FE 'tkGooie' Utilities'MATHtools' group
"Lenders'
|
The GUI interface to QUICKLY 'compound' interest for various sub-periods of a year --- showing that bankers could not triple their money in a year at 100% annual interest --- even when broken up and 'compounded' every millisecond. Larger, hi-res image is below. |
FE Home Page >
FE Downloads Page >
FE 'tkGooies' Description Page >
FE 'tkGooies' 'MATHtools' Page >
This
'tkLendersCompoundInterestDreamCrushed'
code Page
|
INTRODUCTION to Tcl-Tk script For several years now (circa 2013-2015), I have been planning to make a Tk GUI that quickly performs some 'compound interest' calculations that clearly demonstrate that there is a definite limit to how much interest a lender could collect from a borrower, by 'compounding' a given annual interest rate over a year. A Review of Compounding Interest: Note that by compounding of an annual interest rate 'r', the lenders historically mean 'chopping up' that interest rate into equal amounts --- such as 12ths for 12 months of the year. Then, instead of applying 'r' once, at the end of the year, to the principal P, the lender applies r/12 to P in the first month getting an amount owed at the end of the first month, say S1. Then S1 is the original principal P plus r/12 times P --- or P * (1 + r/12). Now the lender takes that amount to be the new principal to be lent with interest for another month --- and we calculate the amount S2 owed at the end of the 2nd month. So, the interest for the 2nd month is S1 * r/12, and that is added to the principal S1 at the start of the 2nd month. This means that
S2 = S1 + S1 * r/12 where we used the expression for S1 that we found above. You may see the start of a pattern here, but let's take this one more month. We want to calculate the amount owed at the end of month 3, say S3. The lender takes the amount owed at the end of month 2 to be the new principal --- which is lent with interest for another month. The lender calculates the number S3 owed at the end of the 3rd month as follows. The interest for the 3rd month is S2 * r/12, and that is added to the principal S2 at the start of the 3rd month. This means that, using the expression the lender got for S2 above, the lender calculates
S3 = S2 + S2 * r/12 By the end of the 12th month, the lender wants to know what the borrower would owe --- which would be given by an expression like |
S12 = P * (1 + r/12) * (1 + r/12) * ... 9 more times ... * (1 + r/12)
|
which in more compact, exponential notation is S12 = P * (1 + r/12)^12 where '^12' denotes multiplying the number in parentheses by itself 12 times. A Trip Back to the Middle Ages It was not so hard for the lender of the Middle Ages to carry out computations for compounding twice a year (every 6 months) --- or 3 times a year (every 4 months) --- or 4 times a year (quarterly). Let us take a simple value for r --- 1, corresponding to annual interest of 100 percent. Although this may sound like a quite-high lending interest in the 21st century, back in the Middle Ages, when people were lucky to live past 30 years old, the lender must have thought the probablity in getting his money back within a year was rather low. A year must have seemed like a long time to lend out money to a person. 100 percent interest probably would seem, to the lender, to be justified --- in light of the risk he was taking. Besides, the 'payday lenders' of the 21st century would consider 100% a quite reasonable annual interest rate. At 100 percent interest, the lender would get results like the following --- for the amount owed at the end of one year: |
annual interest: P * (1 + 1) = 2.0 * P
every 6 months: P * (1 + 1/2) * (1 + 1/2) =
P * 1.5^2 = 2.25 * P
every 4 months: P * (1 + 1/3) * (1 + 1/3) * (1 + 1/3) =
P * 1.333^3 = 2.368 * P
every 3 months: P * (1 + 1/4) * (1 + 1/4) * (1 + 1/4) * (1 + 1/4) =
P * 1.25^4 = 2.441 * P
|
The lenders of the Middle Ages must have been very intrigued by this upward progression in the amount owed at the end of a year. What if they 'compounded' interest every month? every week? every hour? every second? It must have looked to them like 'the sky is the limit'. Even if they used a lower annual interest rate --- like 50 percent or 25 percent --- it looked like they would be in for a huge pay-day at the end of a year. But they were in for a grand letdown. The sky was not the limit. 'e' was the limit. Or, before Euler gave it a single character name, a factor of 2.718 (or slightly greater) was the limit. Here is a quote from the book "e:The Story of a Number" by Eli Maor (page 187): The origins of determining this limit "seem to go back to the 16th century, when it was noticed that the expression (1 + 1/n)^n, appearing in the formula for compound interest tends to a certain limit --- about 2.71828 --- as n increases." Maor goes on to say
"Thus 'e' became the The Swiss mathematician Euler is credited, in math texts, with assigning the lower-case letter E as a symbol to represent that limit. In fact, Maor, in his book on 'e', on page 153, points out: "we owe to Euler many of the mathematical symbols in use today, among them 'i', the Greek letter pi, 'e', and 'f(x)'." On page xiii of his book on 'e', Maor points out that "Someone --- we don't know who or when --- must have noticed the curious fact that if a principal P is compounded n times a year ... at an annual interest rate of r, and if n is allowed to increase without bound, the amount of money S " at the end of a year --- found from S = P * (1 + r/n)^n --- "seems to approach a certain limit. This limit, for P = 1 and r = 1 [that is, 100% interest] ... is about 2.718." To cut short this introduction here, I summarize by saying that I decided to make a Tk GUI that would have made it easy for any lender of the Middle Ages to see what kind of return he would get on his money by taking 'compounding' to its extremes. If you want more information on interest compounding or the 'natural number' denoted by 'e', you can do a WEB SEARCH on keywords such as In Maor's book on 'e', Chapter 3, titled 'Financial Matters', may be of interest. Several brief tables of calculations are shown there. PLANNED LAYOUT OF THE GUI: As I have done with other Tk scripts that I have written in the past year or so, I laid out a 'text image' of the GUI --- to aid me as I coded the frames and widgets. I used the following conventions to make the sketch, with a text editor. |
SQUARE-BRACKETS indicate a comment (not to be placed on the GUI).
BRACES indicate a Tk 'button' widget.
A COLON indicates that the text before the colon is on a 'label' widget.
UNDERSCORES indicate a Tk 'entry' widget.
CAPITAL-O indicates a Tk 'radiobutton' widget.
CAPITAL-X indicates a Tk 'checkbutton' widget (if any).
<---O---> indicates a horizontal Tk 'scale' widget (if any).
According to those conventions,
I created the following 'text sketch'.
FrameNames
VVVVVVVVVV
-----------------------------------------------------------------------------
tkLendersCompoundInterestDreamCrushed ('e' --- about 272% --- Is The Limit)
[window title]
-----------------------------------------------------------------------------
.fRbuttons {Exit} {Help}
.fRcontrols1 Desired 'base'
annual interest (%): 100.00__ [This figure may be shown in a 'disabled' entry widget.]
.fRcontrols2 Compounding
period: O annual O monthly O weekly O daily O hourly O by minute O by second
.fRmsg [... Messages to the user can be displayed here on a label widget ...]
.fRresult Actual annual
interest (%): [ Calculated interest is shown in a text widget here. ]
[The following 'plot' frames may be implemented in the future.]
.fRplotcntl {Plot value of {Backgd {Line {Title-Labels {TicMarks
(1 + 1/n)^n} Color} Color} Color} Color}
.fRplot -----------------------------------------------------------------------------
| |
| |
| |
| ['Canvas' for displaying a plot of (1 + 1/n)^n against n.] |
| |
| [eventually] |
| |
| |
| |
-----------------------------------------------------------------------------
|
From the diagram above, I could see that this GUI will contain about:
Assembling the pieces Now it was a matter of putting the pieces together. I took 'code-pieces' from some of my other Tk scripts that 'draw' in an image area on a Tk canvas. I ended up with the following GUI as an initial display. |
|
Note that I have provided several 'radiobutton' widgets by which to specify a compounding number 'N' --- mostly for 'natural' compounding-periods for which the calculation of 'the total amount owed at the end of a year' is tedious to compute manually. (Logarithm tables, that came along around the 1600's, could have provided some computational relief to the late Middle Agers.) I chose values of 'N' for the following seven compounding periods. They result in the following computations based on an interest rate of 100 percent for the period. |
annual: (1 + 1)
monthly: (1 + 1/12)^12
weekly: (1 + 1/52)^52
daily: (1 + 1/365)^365
hourly: (1 + 1/8760)^8760 where 8760 = 365*24
by the minute: (1 + 1/525600)^525600 where 525600 = 8760*60
by the second: (1 + 1/31536000)^31536000 where 31546000 = 525600*60
|
Super-quick calculation As the initial instruction on the message line indicates, a click on a radiobutton causes the compound interest calculation (in a fraction of a second), and the resulting 'actual annual interest percent' is shown in a 'RESULT' line of the GUI. Wouldn't those Middle Age lenders (bankers and 'dark-ages racketeers' and such) have loved to be able to use Tcl-Tk?
Implementing some Color Buttons If I ever add a plotting option to this GUI, the color buttons (next to the 'Exit' and 'Help' buttons) will call on an 'external' color-selector-GUI script to set those colors. You can make that color-selector script by cutting-and-pasting the code from the page that offers a non-obfuscated color selector GUI on this site. You can see the code at the bottom of the Tk script to see how the name and location of the color selector script is set. DESCRIPTION OF THE CODE Below, I provide the Tk script code for this 'tkLenders CompoundInterestDreamCrushed' math-education or math-tool 'app'. I follow my usual 'canonical' structure for Tk code, for this Tk script: |
0) Set general window & widget parms (win-name, win-position,
win-color-scheme, fonts, widget-geometry-parms, win-size-control).
1a) Define ALL frames (and sub-frames, if any).
1b) Pack ALL frames and sub-frames.
2) Define & pack all widgets in the frames, frame by frame.
Within each frame, define ALL the widgets.
Then pack the widgets.
3) Define keyboard and mouse/touchpad/touch-sensitive-screen action
BINDINGS, if needed.
4) Define PROCS, if needed.
5) Additional GUI initialization (typically with one or more of
the procs), if needed.
|
This Tk coding structure is discussed in more detail on the page A Canonical Structure for Tk Code --- and variations. This Tk coding structure makes it easy for me to find code sections --- while generating and testing this script, and when looking for code snippets to include in other scripts (code re-use). Experimenting with the GUI As in all my scripts that use the 'pack' geometry manager (which is all of my 100-plus Tk scripts, so far), I provide the four main 'pack' parameters:
on all the 'pack' commands for the frames and widgets. I think I have found a good setting of the '-side', '-anchor', '-fill', and '-expand' parameters on the 'pack' commands for the various widgets of this GUI. In particular ... Button and label and entry widgets stay fixed in size and relative-location if the window size is changed by the user --- and, if I implement plotting (someday), the 'canvas' widget will expand/contract appropriately when the window is resized. I allow the window to be resized --- in anticipation of implementing the plotting canvas someday --- and in planning to allow the canvas (the plot) to be resized when the user resizes the GUI window. If anyone wants to change the way the GUI configures itself as the main window size is changed, they can experiment with the '-side', '-anchor', '-fill', and '-expand' parameters on the 'pack' commands for the various widgets --- to get the widget behavior that they want. Or they can implement a 'wm' (window manager) command to make the GUI un-resizable. Simply un-comment the line: wm resizable . 0 0 --- Additional experimentation with the GUI: You could change the fonts used for the various GUI widgets. For example, you could change '-weight' from 'bold' to 'normal' --- or '-slant' from 'roman' to 'italic'. Or change font families. In fact, you may NEED to change the font families, because the families I used may not be available on your computer --- and the default font that the 'wish' interpreter chooses may not be very pleasing. Furthermore, there are variables used to set geometry parameters of widgets --- parameters such as border-widths and padding. And you could change the '-relief' values for frames and widgets. Feel free to experiment with those 'appearance' parameters as well. Some features of the code There are plenty of comments in the code to describe what most of the code-sections are doing. 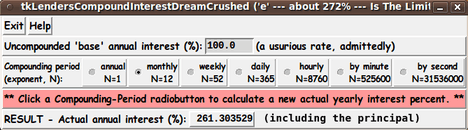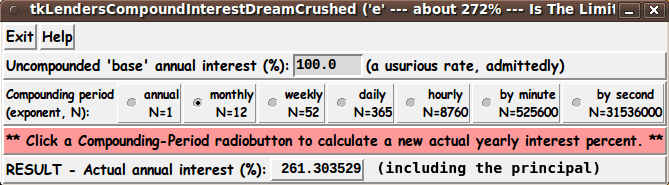The main calculations are done in a 'calc_interest' proc. See the top of the 'PROCS' section for a list of the procs used in this Tk script. See comments in the procs for details on the purpose of each proc and for details on the methods by which each proc was implemented. Below is a quick overview of the procs --- to give an idea of the 'guts' of this utility. There are only three procs in the initial implementation: |
- 'calc_interest' - called by button1-release bindings on the
compounding-period radiobuttons.
- 'advise_user' - called in the 'Additional GUI Initialization'
section at the bottom of the Tk script
- 'popup_msgVarWithScroll' - called by 'Help' button
|
If I implement plotting, there will be procs like the following: |
'setMappingVars_for_px2wc' - called by a 'draw_plot' proc.
Sets up constants to be used in converting
a 'world coordinate' to a 'pixel coordinate'
on the Tk canvas.
This proc takes the coordinates of an UpperLeft (UL)
point and a LowerRight (LR) point --- in BOTH
'world coordinates' and 'pixel coordinates' and
sets some global variables to be used by the
other drawing procs --- mainly the ratio:
the number-of-pixels-per-world-coordinate-unit,
global variable 'PXperWC'
'Xwc2px' - converts an x world-coordinate to pixel units,
in various draw-lines and draw-text procs.
'Ywc2px' - converts a y world-coordinate to pixel units,
in various draw-lines and draw-text procs.
*****************************
End of Drawing utility procs.
*****************************
***************************
Color-Button utility procs:
***************************
'set_background_color' - Called by the background color button.
'set_line_color' - Called by the plot lines (and points) color button.
'set_title-labels_color' - Called by the plot title (and labels) color button.
'set_ticmarks_color' - Called by the ticmarks color button.
'update_button_colors' - Sets the color of the 4 color buttons.
**********************************
End of Color-Button utility procs.
**********************************
|
To potential Tcler's It is my hope that the copious comments in the code might help Tcl-Tk coding 'newbies' get started in making GUI's like this. Without the comments --- especially in the procs --- the code might look even more cryptic than it already is. Without the comments, potential young Tcler's might be tempted to return to their iPhones and iPads and iPods (and Samsung and other equivalents) --- to look for videos of late-night news-dissection hosts, such as dissecting the current political scene in the United States. While it is tempting to 'tune in' to this exposure of the soft, white under-belly of American Idiocy, please break away occasionally to try some coding using the Tcl-Tk 'wish' interpreter. The Tcl-Tk script CODE Here is a link to CODE for the Tk script 'tkLendersCompoundInterestDreamCrushed_ eIsTheLimit.tk'. With your web browser, you can 'right-click' on this link --- and in the menu that pops up, select an option like ' Save Link Target As ... ' to save this file to your local computer. Then you can rename the file to remove the '.txt' suffix. Make sure that you have execute permission set on the file --- in order to execute the script. |
|
Some possible FUTURE ENHANCEMENTS I have indicated above several of the enhancements that I am considering adding someday:
|
.fRcontrols1 Uncompounded 'base' 100% 50% 25% 20% 10% 5%
annual interest (100/M %): O (M = 1) O (M = 2) O (M = 4) O (M = 5) O (M = 10) O (M = 20)
|
Note that the 'calc_interest' proc will be changed to evaluate the expression |
( 1 + 1/(M*N) )^N where 1/M is the annual interest rate as a fraction (not percent)
|
Note that this expression bears a close resemblance to the sequence that defines the 'natural number' 'e'. In fact, we can rewrite this expression as |
( 1 + 1/(M*N) )^(M*N)*1/M = ( ( 1 + 1/(M*N) )^(M*N) )^1/M
|
If we replace the integer M*N by a symbol K, representing integers, then it looks like we have the sequence of numbers that define 'e', but each one raised to the 1/M power. This is actually the Mth-root of each of the numbers in the sequence, and we can expect the sequence on the left to approach the Mth-root of 'e': |
approaches
( ( 1 + 1/K )^K )^1/M --------> e^1/M as K 'goes to infinity'
_____________
the sequence
that defines
'e'
|
If I code this radiobuttons enhancement, I will probably code the XY plotting enhancement --- the 'canvas' widget --- at the same time. The plot proc will then calculate e^1/M and show that for any given M, the sequence of numbers ( 1 + 1/(M*N) )^N rises up to meet a horizontal line at the height e^1/M (the Mth-root of 'e') on the graph. In other words, we show that if a lender is lending money at an interest rate of 100/M percent --- and if the lender offers the money at smaller and smaller compounding intervals --- the 'actual annual interest' approaches a number given by the Mth-root of 'e': (e^1/M - 1)*100 percent not including the principal. Note that e^1/M is always greater than 1, but approaches 1 as M goes to infinity. This makes sense because M was the divisor of a 100% interest rate --- and as M goes to infinity, we are emulating an interest rate closer and closer to zero. --- One advantage of this Tk script is that it is 'open' code --- available to anyone for enhancement. So if you would like to take a different approach to approximating 'e' --- or the various interest-versus-principal results, you are welcome to take this code and build on it. IN CONCLUSION As I have said on other code-donation pages on this site ... There's a lot to like about a utility that is 'free freedom' --- that is, no-cost and open-source so that you can modify/enhance/fix it without having to wait for someone else to do it for you (which may be never). A BIG THANK YOU to Ousterhout for starting Tcl-Tk, and a BIG THANK YOU to the Tcl-Tk developers and maintainers who have kept the simply MAH-velous 'wish' interpreter going. |
|
Bottom of this web page for
To return to a previously visited web page location, click on the
Back button of your web browser a sufficient number of times.
OR, use the History-list option of your web browser.
< Go to Top of Page, above. >Page history:
This FE web page was created 2016 Mar 24.
NOTE: |