|
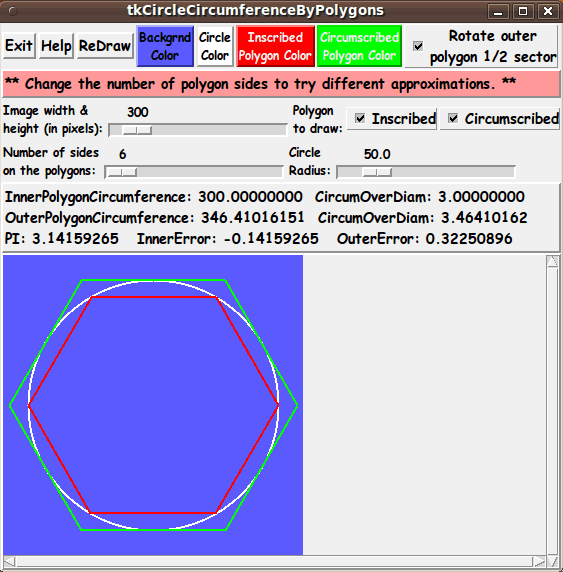
Before capturing this image, I changed the 'format' statements in
the script that determine the number of decimal digits to display.
Since I had room in the results-message area, I changed from 6 digits
to 8 digits.
Execution time:
The drawing and computations complete almost immediately after clicking
on the 'ReDraw' button --- even if you request hundreds of sides for
the two polygons.
Wouldn't Archimedes (and Galileo and Newton and Euler and the Bernoulli's
and Gauss and Lagrange and Laplace and Weierstrass and Poincare and Riemann
and ...) have loved to be able to use Tcl-Tk?
I wonder what wonders Archimedes would have performed
with the 'wish' interpreter at his disposal?
Sure beats drawing in the sand.
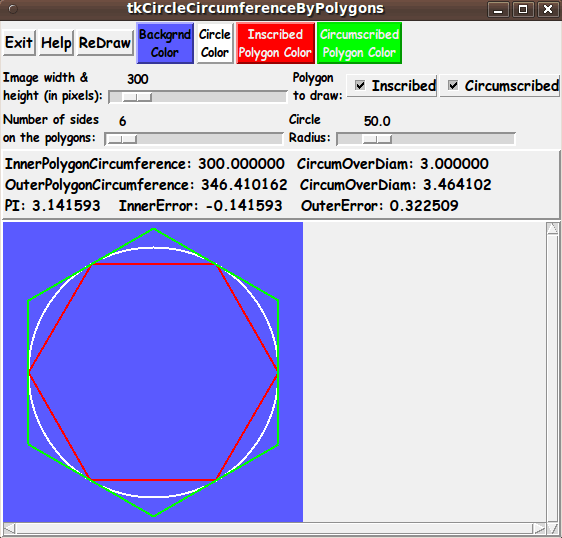
Changing the Radius
(to confirm that pi is a constant, independent of circle size)
The user can change the radius 'scale' widget repeatedly (and
click on the 'ReDraw' button after each change) to see that the two
ratios (polygon circumference to diameter) do not change.
Of course, this could be predicted by careful examination of algebraic
formulas that summarize how the calculations are performed.
A radius factor in the numerator and denominator cancel out.
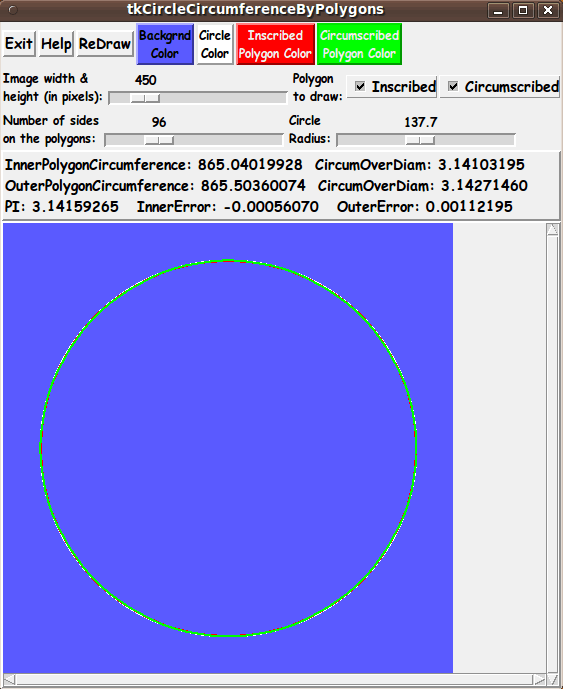
Increasing the Number of Sides
(a lot)
The results we see with this tool suggest that we can 'squeeze down'
to a unique number --- called pi.
(By examining the algebraic formulas for the two polygon circumferences,
it should be provable that the difference between the two polygon
circumferences goes to zero --- and one is bounded above and always
increasing, while the other is bounded below and always decreasing.
So each sequence goes to a unique limit --- the same limit.)
Other changes to try:
(to push the accuracy of the ratios
to many decimal digits)
You can change the NumSides to 360, so that the central angle of
each sector of the polygons is exactly one degree.
These polygons are almost indistinguishable from the circle.
You will see that the errors are out at the 6th decimal digit.
Five decimal digits is more than enough accuracy for most engineering work.
A couple of quotes from a 2009 document 'Computing the Digits in Pi' by
Carl Offner (University of Massachusetts, Boston):
"I asked a civil engineer how many digits of pi he would actually
ever need. After thinking about it for a while, he agreed with me
that 5 was probably pushing it."
"It requires ... 39 digits of pi in order to compute the circumference
of a circle of radius 2 × 10 to the 25th meters (an upper bound on the
distance traveled by a particle moving at the speed of light for
20 billion years, and as such an upper bound on the
radius of the universe) with an error of less than 10 to the -12 meters
(a lower bound for the radius of a hydrogen atom)."
Borwein and Borwein (1984)
"But what do astronomers and astrophysicists really need?
I spoke to two recently. One had used whatever the pi key on
her calculator produced -- at most, 10 digits.
The other thought that 7 or 8 places was the most he'd
ever seen the need for.
And even in quantum field theory, where there are physical constants
that are known to an astounding accuracy of 12 or 13 decimal places,
it wouldn't really help to know pi to any greater accuracy than that."
A computer engineering viewpoint:
"In recent years, the computation of the expansion of pi has assumed
the role as a standard test of computer integrity.
If even one error occurs in the computation, then the result will
almost certainly be completely in error after an initial correct section.
On the other hand, if the result of the computation of pi to even 100,000
decimal places is correct, then the computer has performed billions of operations
without error.
For this reason, programs that compute the decimal expansion of pi
are frequently used by both manufacturers and purchasers of new
computer equipment to certify system reliability."
Bailey (1988)
Scrollable Canvas
(and big image area)
Note that the canvas in the GUI has vertical and horizontal scrollbars
--- and you can set a large image area size with the image-size scale widget.
So you can set a very large image area in which to do the drawings.
And if you think the max-pixels of the image-size scale widget is not big
enough for you, you can edit the Tk script and change the '-to' parameter
on the 'scale' widget for the image size.
Distance units
You can think of the radius being specified in whatever units you want
--- feet, yards, meters, kilometers.
Hence you can imagine drawing a huge circle on a big flat beach or a
flat river delta --- a circle with a radius of 100 meters or more.
You pound a stake in the ground and attach a rope that is 100 meters long.
Then you use the other end of the rope to 'scribe' a big circle on the beach.
Then you see how many times you can measure off the rope distance (the radius)
on that scribed circle.
It should be two-pi times ( 6.28... ) --- 6 rope lengths
plus a little more than a quarter of the rope.
---
Implementing the Color Buttons
The 2 color buttons call on an 'external' color-selector-GUI script to
set those colors.
You can make that color-selector script by cutting-and-pasting the code from
the page that offers
a non-obfuscated color selector GUI
on this site.
You can see the code at the bottom of the Tk script to see how the
name and location of the color selector script is set.
DESCRIPTION OF THE CODE
Below, I provide the Tk script code for this
'tkCircleCircumferencesByPolygons' 'app'.
I follow my usual 'canonical' structure for Tk code, for this Tk script:
|