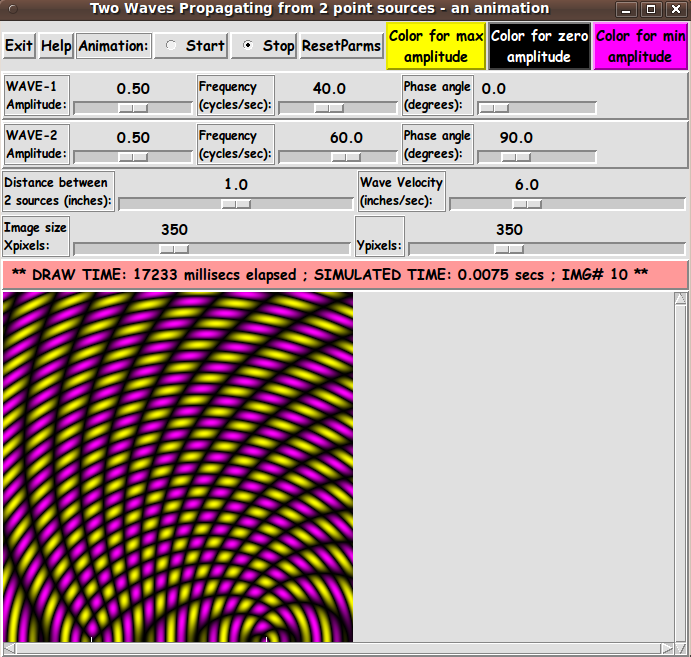
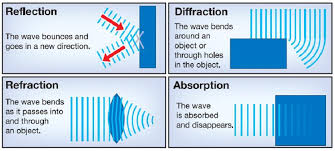
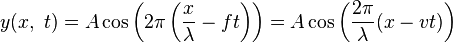|
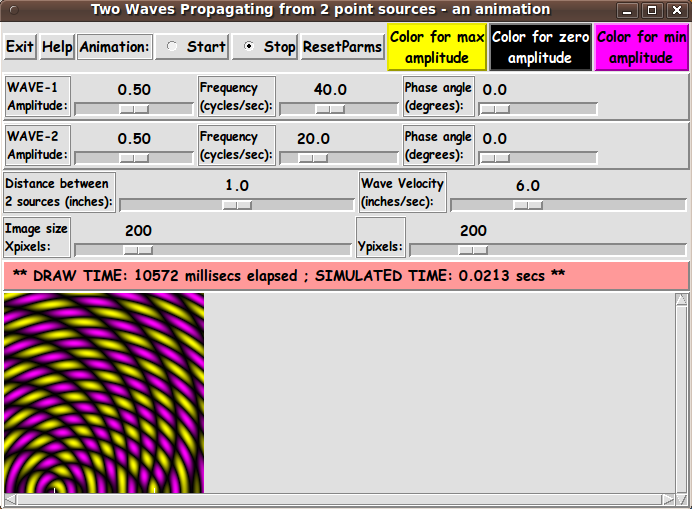
where there are 3 terms in the sin function and where
A(i) and ph(i) are constants for wave i --- 'A' being
an amplitude factor and 'ph' being a phase angle.
(We allow for two different 'initial' phase angles for the 2 waves.
In other words, we allow for simulating 2 waves that are NOT
in sync at their sources, even when their two frequencies are equal.)
f(i) and L(i) are the frequency and wave-length of wave i.
The term ( 2 * pi * f(i) * t ) represents the sinusoidal variation
with time, t, of the wave amplitude at any point (x,y) --- converted
to radians.
The term ( 2 * pi * r(i,x,y) / L(i) ) represents the number of
wave-lengths from the source-point to the point (x,y) --- converted
to radians.
r(i,x,y) represents the distance from the source-point of wave i.
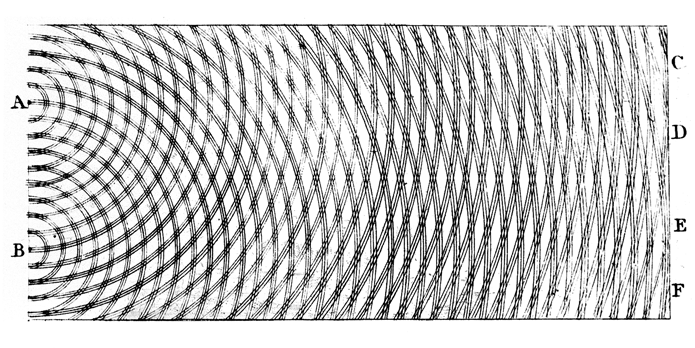
Let us say (x1,y1) and (x2,y2) are the 2 source points. Then
r(1,x,y) = sqrt( (x-x1)^2 + (y-y1)^2 )
and
r(2,x,y) = sqrt( (x-x2)^2 + (y-y2)^2 )
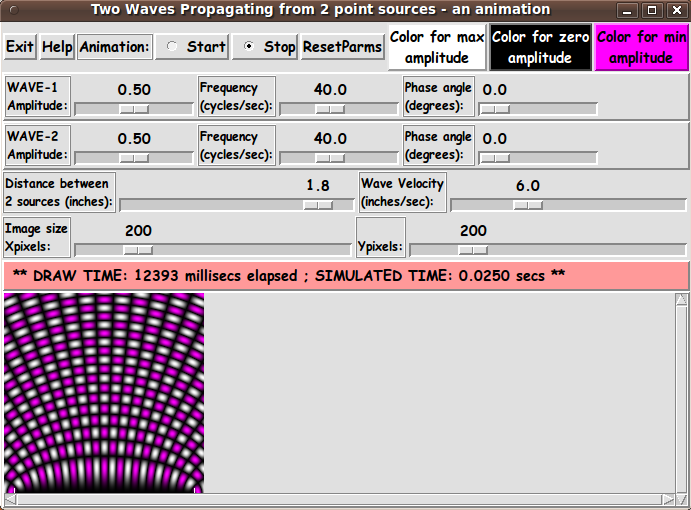
We will let the 2 source points be on the bottom of the
image rectangle at y=0.
We will let the origin (0,0) be in the middle of the bottom
of the rectangle.
We let the two source points be a distance 'd' on either side of
the origin.
The resultant amplitude (RA) of the 2 merged waves at time t
and at point (x,y) is given by
A(1,x,y,t) + A(2,x,y,t).
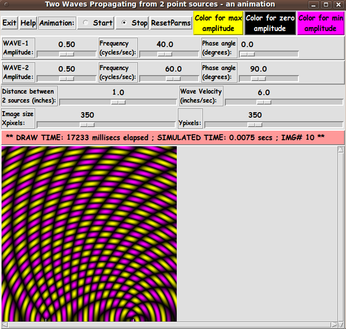
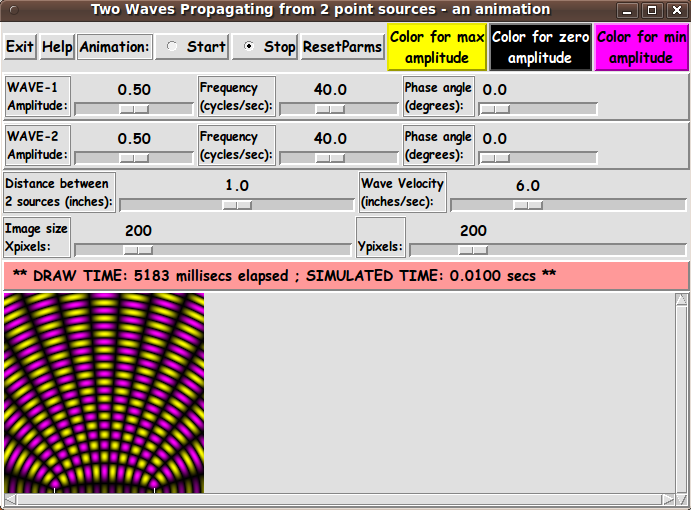
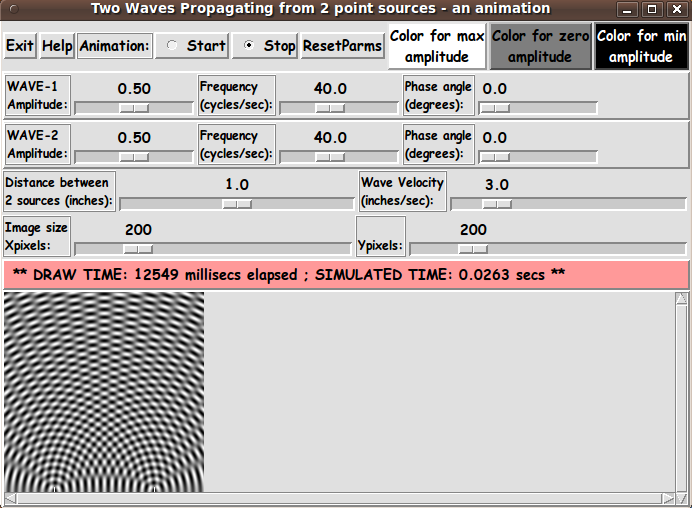
The Tk GUI allows the user to specify positive constants for the
numbers f(i), L(i), A(i), ph(i), and 2d (the distance between the
two point sources).
(Actually, we let the user specify wave-velocity, v, rather
than L(1) and L(2).
We calculate L(i) = v / f(i).)
Method of Math Conversion of
the Resultant-Amplitude to Color:
The amplitude of the waves are depicted with colors interpolated
between a 'max-color' and a 'min-color'.
In fact, we allow for specifying a 3rd 'zero-color'.
For positive amplitudes, we interpolate between 'max-color'
and 'zero-color'.
For negative amplitudes, we interpolate between 'min-color'
and 'zero-color'.
So the Tk GUI is to have 3 buttons by which to specify the
- max-color
- zero-color
- min-color
We use the sum of the 2 max-amplitudes
Asum = A(1) + A(2)
to do the interpolation.
When resultant amplitude
RA = A(1,x,y,t) + A(2,x,y,t)
is positive, we get the color for RA from
|