FE 'tkGooie' Utilities 'MATHed' subgroup of the 'MATHtools' group A Tk GUI script demonstrating a 'Half-Angle' theorem: For a given Circle Chord (or arc), the Subtending Angle at the Center of the Circle is Twice Any Subtending Angle at the Circumference. ( Code for a GUI to demonstrate what is sometimes called the 'inscribed angle' or the 'central angle' theorem. ) (FE = Freedom Environment)

GUI which allows the user to drag the point C on the circumference of the circle and watch that the angle at C is ALWAYS half the angle at A, the center of the circle.

FE Home Page > FE Downloads Page >

FE 'tkGooies' Description Page >

FE 'tkGooies' 'MATHtools' Menu >

FE 'tkGooies' 'MATHed' Menu >

This
'tkCircleChord_TheSubtendingAngleAtCenter
IsTwiceTheAngleAtCircumference'
Page

INTRODUCTION to Tcl-Tk script 'tkCircleChord_TheSubtendingAngleAtCenter IsTwiceTheAngleAtCircumference' In the 2013-2016 time frame, I started making some 'tkGooie' scripts for a 'MATHed' (Mathematics Education) toolchest --- scripts such as: Thales' Theorem: A Triangle Inscribed in a Semicircle is always a Right Triangle An Eratosthenes Prime Sieve (pixels in a resizable canvas) Approximating Circle Circumference By Polygons (a demonstration of Archimedes' method for approximating PI --- the ratio of the circumference of a circle to its diameter) In my readings of various books popularizing math and, in particular, books containing discoveries in plane (Euclidean) geometry, such as the book 'Trigonometric Delights' by Eli Maor, in particular, Chapter 6, I ran across static images representing the ancient theorem that says: Given a chord (or arc) in a circle, the angle subtending that chord whose vertex is at the CENTER of the circle is always twice as large as ANY angle subtending the same chord and with vertex ANYWHERE on the CIRCUMFERENCE of the circle. This is quite a mouthful, but it is hard to shorten the name of this theorem and convey all the aspects of this theorem --- which involves a circle, a chord, a subtending 'central angle', and any of an infinite number of subtending 'circumference angles'. One nickname that has been given to this theorem, inadequate though it is in describing the theorem, is the inscribed angle theorem (Reference: wikipedia.org). Another nickname is the central angle theorem (Reference: mathopenref.com). I personally think that 'double angle' theorem (or 'half angle' theorem) would be a better short name, but the phrase 'double angle' is already used for various trigonometric formulas involving the sine and cosine. Similarly, 'half angle' is already used for various trigonometric formulas ('identities') involving the sine and cosine. --- It turns out that the older 'Thales theorem' mentioned above (which involved a triangle inscribed in a semi-circle) is a special case of this 'inscibed angle theorem'. The proof of Thales' theorem follows quickly because the diameter of the semi-circle can be considered as the central angle (which is 180 degrees), and the angle opposite that diameter is the 'inscribed angle', which, according to the 'inscribed angle theorem' is half of 180 or 90 degrees (a right angle). There are many web sites with more information on the 'inscribed angle' or 'central angle' theorem. So if you want to see a variety of discussions of this theorem, you can do a WEB SEARCH on keywords like inscribed angle theorem, OR central angle theorem If you can deal with the annoying popups and advertisements, one web site that is rife with math results is the 'Cut The Knot' site --- which has a page on the Central Angle Theorem --- with a proof done with complex numbers. In any case, with the Tk script (whose code is presented on this page), I was seeking to make the demonstration of the validity of the Central Angle Theorem an interactive and dynamic (semi-animated) experience --- using Tcl-Tk. Around 2016, with the advent of Javascript enhancements associated with HTML 3.0, some dynamic, interactive demos of math results started appearing on the internet, such as the 'Wolfram Demonstrations Project'. Here is an animated demonstration of the Central Angle Theorem at 'demonstrations.wolfram.com'. In addition, the Wolfram 'MathWorld' site has a couple of 'static image' pages on the 'Inscribed Angle' and the 'Central Angle'. One feature of the 'tkGooie' presented on this page is that it comes bundled within a 'tkGooies' menu-driven system that can be installed on a computer --- or on a file server that serves files to multiple computers. Another feature of the 'tkGooies' is that I generally provide more control of colors than one sees in many math demo utilities. 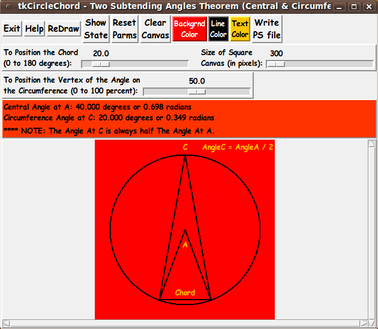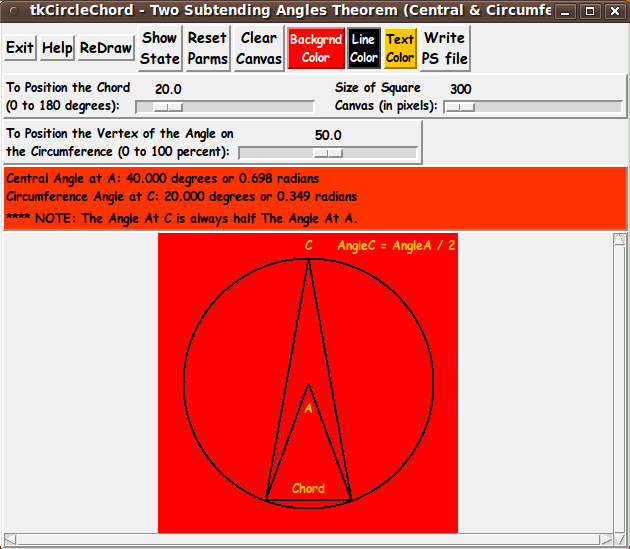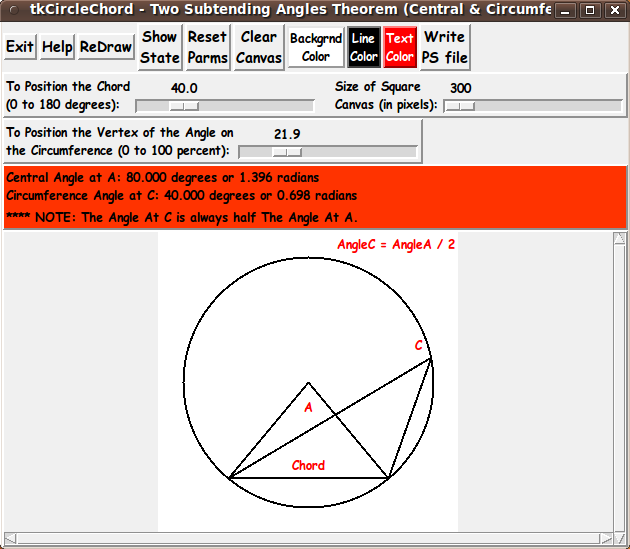Basic Goals of the Tk Script: My purpose for this Tk GUI script is/was to generate a circle with a chord (at the end-points of an arc on the circle) that is drawn across the circle. In addition, a 'central angle' and an 'inscribed angle' are to be drawn subtending that chord --- AND the user is to be able to easily change the position (end-points) of the chord, and the position of the vertex of the 'inscribed angle', which lies on the circumference of the circle. To allow for pretty precise control in drawing these points, I decided to use 2 Tk 'scale' widgets to adjust the position of the chord, and the position of the vertex of the 'inscribed angle'. (See the GUI image at the top of this page --- or larger images below.) The drawings of the circle are to be done in a resizable square image area --- in a Tk 'canvas' widget. The GUI is to automatically delete-and-redraw (for the user) any changed points --- and delete-and-redraw the two angles (and show that the 'central angle' is ALWAYS twice the 'inscribed angle'). PLANNED LAYOUT OF THE GUI: As I have done with other Tk scripts that I have written in the past year or so, I laid out a 'text image' of the GUI --- to aid me as I coded the frames and widgets. I used the following conventions to make the sketch, with a text editor.

  SQUARE-BRACKETS indicate a comment (not to be placed on the GUI).
  BRACES          indicate a Tk 'button' widget.
  A COLON         indicates that the text before the colon is on a 'label' widget.
  <---O--->       indicates a Tk 'scale' widget (if any).
  CAPITAL-X       indicates a Tk 'checkbutton' widget (if any).
  CAPITAL-O       indicates a Tk 'radiobutton' widget (if any).
  UNDERSCORES     indicate a Tk 'entry' widget (if any).


  According to those conventions,
  I created the following 'text sketch'.


 FrameNames
 VVVVVVVVVV
              -----------------------------------------------------------------------------
              tkCircleChord - Two Subtending Angles Theorem (Central & Circumference)
              [window title]
              -----------------------------------------------------------------------------

 .fRbuttons   {Exit} {Help} {ReDraw} {Show   {Reset  {Clear  {Backgd  {Line   {Text   {Write
                                      State}  Parms}  Canvas  Color}   Color}  Color}  PS File}

 .fRchord     Position   0                    180   Size of Square      300          4000
              of Chord:  <-----------O---------->   Canvas (in pixels): <-------O------->

 .fRcircum    Position Vertex  -50                +50
              on Cirumference: <----------O--------->
 
 .fRinfo      [ .......... to contain a stack of label widgets ......................... ]

 .fRcanvas    ----------------------------------------------------------------------------A
              |                                                                           |
              |                                                                           |
              |                                                                           |
              |  [Area in which a Square Canvas (with scrollbars) is centered ---         |
              |   for displaying the circle, chord, and two subtending angles.]           |
              |                                                                           |
              |                                                                           |
              |                                                                           |
              |                                                                           |
              <-------------------------------------------------------------------------->V

Perhaps some aspects of the sketch could use a little more explanation:

  A combination of VERTICAL-BAR CHARACTERS AND HYPHEN (or UNDERSCORE) CHARACTERS,
  that outline a RECTANGULAR SHAPE, are used to indicate either a Tk 'canvas' or
  a Tk 'listbox' widget or a Tk 'text' widget.

  A LINE (HYPHENS or VERTICAL-BARS) WITH AN 'ARROW-HEAD' AT EACH END indicates
  a Tk 'scale' widget --- or a 'scrollbar' widget.

  SCROLL-BAR 'ARROW-HEADS' (for a 'canvas', 'listbox', or 'text' Tk widget)
  are drawn as follows:

   UP    ARROW-HEAD   is drawn with a CAPITAL-A.
   DOWN  ARROW-HEAD   is drawn with a CAPITAL-V.
   LEFT  ARROW-HEAD   is drawn with a LESS-THAN sign.
   RIGHT ARROW-HEAD   is drawn with a GREATER-THAN sign.

  UP-and-DOWN    ARROW-HEADS  at the right/left of a box shape indicate
  a VERTICAL SCROLL-BAR there.

  LEFT-and-RIGHT ARROW-HEADS  at the bottom/top of a box shape indicate
  a HORIZONTAL SCROLL-BAR there.

  The arrow-heads on a horizontal scrollbar are joined by hyphens, rather than
  underscores.

From the diagram above, I could see that this GUI will contain about: 10 'button' widgets 4 'label' widgets (at least) 3 'scale' widgets 1 'canvas' widget (with x-y scrollbars) 0 'entry' widgets 0 'checkbutton' widgets 0 'radiobutton' widgets 0 'listbox' widgets 0 'text' widgets Assembling the pieces (The GUI) Now it was a matter of putting the pieces together. I took 'code-pieces' from some of my other Tk scripts that 'draw' in an image area on a Tk canvas and use a 'scale' widget --- in particular, from my Thales' Theorem script. I ended up with the following GUI as an initial display.

Note that I have provided 3 color buttons on the GUI so that the user can control : the background color of the image area the color of the lines drawn (the circle, the chord, and the angle sides) the color of text-characters that are placed on the 'canvas'. The message area just below the 'scale' widgets shows the user the current values of the 'central angle' and the 'inscribed angle' --- in degrees and radians. 'Without loss of generality', we draw the chord horizontally --- because for any circle with a chord in it, we could always rotate the circle so that the chord is horizontal (parallel with the edge of a sheet of paper or the edge of a computer screen, say). 'Without loss of generality', we draw a 'unit circle' --- a circle with radius one unit --- whatever that unit is. We can do this because, for any given circle, we can take its radius as our unit of measure --- so the circle will always have radius equal to one. By default, the GUI starts with an initial chord --- and with the 'central angle' drawn above that chord --- and with the 'inscribed angle' drawn with its vertex directly above the center of the circle. A 'ShowState' button at the top of the GUI displays a popup text window that contains numerical information: coordinates of the end-points of the chord (in units relative to the radius of the circle) coordinates of the vertex A of the 'central angle' and the vertex C of the 'inscribed angle' (also in units relative to the radius of the circle) the calculated lengths of the chord, the 2 sides of the 'central' angle, and the 2 sides of the 'inscribed' angle (done using the Pythagorean Theorem --- the square root of the squares of the differences of the x-coordinates and the y-coordintes of the points) the cosines of the 2 angles A and C (by the Law of Cosines formula --- giving a cosine from the lengths of the 3 sides of a triangle.) the 2 angles, A and C, in radians and degrees (done by using the arc-cosine function built into Tcl) NOTE: We are NOT using the GUI to show a proof of the theorem. We use the GUI to VERIFY that the central angle is always twice the inscribed angle --- no matter how we position the chord and how we position the point C. --- Below is an image that was drawn by requesting the point C be 21.9 percent of the way around the circle (from one chord end-point to the other) --- instead of the 50 percent initial default point.

Before clicking the 'Redraw' button, the background color was changed from red to white --- and the text color was changed from orange to red. We could have also changed the image size from 300 pixels to some other size for the square 'canvas'. The 'WritePSfile' button could be used to write out a (color) Postscript file of the image on the canvas. Note that when printing out the image, it will typically be advisable to change the background color of the canvas to white --- to avoid using a lot of ink unnecessarily. Execution time: After clicking on the 'Redraw' button, the computations and drawing complete almost immediately. And after clicking on the 'ShowState' button, the computations complete almost immediately and the results of the computations are shown in a pop-up window almost immediately. Wouldn't Thales and Euclid and Archimedes and Galileo and Newton and Euler and the Bernoulli's and Gauss and Cauchy and Weierstrass and Poincare and Riemann and many many other mathematicians and astronomers and physicists have loved to be able to use Tcl-Tk? I wonder what wonders they would have performed with the 'wish' interpreter at their disposal? Sure beats drawing in the sand or drawing with quill and ink-well --- and beats calculating 'by hand' (excruciatingly slowly). --- Implementing the Color Buttons The 3 color buttons call on an 'external' color-selector-GUI script to set those colors. You can make that color-selector script by cutting-and-pasting the code from the page that offers a non-obfuscated color selector GUI on this site. You can see the code at the bottom of this 'tkCircleChord . . . and central and inscribed angles' script to see how the name and location of the color-selector script is set. You could put the color-selector script in the same directory with this half/double-angle script. DESCRIPTION OF THE CODE Below, I provide the Tk script code for this 'InscribedAngle-and-CentralAngle' 'app'. I follow my usual 'canonical' structure for Tk code, for this Tk script:

  0) Set general window & widget parms (win-name, win-position,
     win-color-scheme, fonts, widget-geometry-parms, win-size-control).

  1a) Define ALL frames (and sub-frames, if any).
  1b) Pack   ALL frames and sub-frames.

  2) Define & pack all widgets in the frames, frame by frame.
              Within each frame, define ALL the widgets.
              Then pack the widgets.

  3) Define keyboard and mouse/touchpad/touch-sensitive-screen action
     BINDINGS, if needed.

  4) Define PROCS, if needed.

  5) Additional GUI initialization (typically with one or more of
     the procs), if needed.

This Tk coding structure is discussed in more detail on the page A Canonical Structure for Tk Code --- and variations. This Tk coding structure makes it easy for me to find code sections --- while generating and testing this script, and when looking for code snippets to include in other scripts (code re-use). Experimenting with the GUI As in all my scripts that use the 'pack' geometry manager (which is all of my 100-plus Tk scripts, so far), I provide the four main 'pack' parameters: '-side' '-anchor' '-fill' '-expand' on all the 'pack' commands for the frames and widgets. I think I have found a good setting of the '-side', '-anchor', '-fill', and '-expand' parameters on the 'pack' commands for the various widgets of this GUI. In particular ... The 'canvas' widget will expand/contract appropriately for a requested (square) image size --- and button, label, and scale widgets stay fixed in size and relative-location as the user changes the window size. If anyone wants to change the way the GUI configures itself as the main window size is changed, they can experiment with the '-side', '-anchor', '-fill', and '-expand' parameters on the 'pack' commands for the various widgets --- to get the widget behavior that they want. --- Additional experimentation with the GUI --- its appearance: You could change the fonts used for the various GUI widgets. For example, you could change '-weight' from 'bold' to 'normal' --- or '-slant' from 'roman' to 'italic'. Or change font families. In fact, you may NEED to change the font families, because the families I used may not be available on your computer --- and the default font that the 'wish' interpreter chooses may not be very pleasing. Furthermore, there are variables used to set geometry parameters of widgets --- parameters such as border-widths and padding. And you could change the '-relief' values for frames and widgets. Feel free to experiment with those 'appearance' parameters as well. Some features of the code There are plenty of comments in the code to describe what most of the code-sections are doing. See the top of the 'PROCS' section of the script for a list of the procs used in this Tk script. See comments in the procs for details on the purpose of each proc and for details on the methods by which each proc was implemented. Below is a quick overview of the procs --- to give an idea of the 'guts' of this utility:

   'ReDraw'                    - Called by the 'ReDraw' button.

   'draw_circle_x1y1_radius'   - Called by the 'ReDraw' proc.

   'draw_line_x1y1x2y2'        - Called by the 'ReDraw' proc.

   'draw_text_x1y1_center'     - Called by the 'ReDraw' proc.

   'draw_point_x1y1_radiusPx'  - Called by the 'ReDraw' proc (if this is used).

   'setMappingVars_for_px2wc'  - Called by the 'ReDraw' proc.

   'Xwc2px'                    - Called by the various 'draw' procs.

   'Ywc2px'                    - Called by the various 'draw' procs.

   'set_background_color0'     - Called by the 'BkgdColor' button.
 
   'set_line_color1'           - Called by the 'LineColor' button.
 
   'set_text_color2'           - Called by the 'TextColor' button.

   'update_button_colors'      - Called by the several 'set_*_color*' procs. 

   'advise_user'               - Called by the 'ReDraw' proc and in the
                                 'Additional GUI Initialization' section at
                                 the bottom of the script.

   'show_state'                - Called by the 'ShowState' button. 

   'writePSfile'               - Called by the 'WritePSfile' button.

   'popup_msgVarWithScroll'    - Called by the 'Help' button to show the
                                 'HELPtext' variable.

The initial drawing on the canvas is performed by the 'ReDraw' proc. See the comments in that proc to see how it is implemented. A fervent hope It is my hope that the copious comments in the code might help Tcl-Tk coding 'newbies' get started in making GUI's like this. Without the comments --- especially in the 'ReDraw' and 'setMappingVars_for_px2wc' and 'Xwc2px' and 'Ywc2px' procs --- the code might look even more cryptic than it already is. Without the comments, potential young Tcler's might be tempted to return to their iPhones and iPads and iPods --- to look for videos of TV news organizations interviewing politicians and their 'surrogates' (and NOT asking obvious follow-up questions). Examples: Where are all the explosives used in car bombs and by suicide bombers and in IED's (Improvised Explosive Devices) coming from? Who is buying them? Who is shipping them? Who is making them? Where are all the rapid-fire weapons used by ISIS and al-Queda and the Taliban --- and various Islamic terrorist groups in Somalia, Nigeria, Mali, Libya, Tunisia, etc. --- coming from? Who is buying them? Who is shipping them? Who are the manufacturers? Russian? Chinese? USA? All three? In what proportions? Mostly USA? Mostly Russian? Mostly Chinese? Where are all the rocket launchers coming from? Who is buying them? Who is shipping them? Who are the manufacturers? Russian? Chinese? USA? All three? In what proportions? Mostly USA? Mostly Russian? Mostly Chinese? Where are all the armored vehicles coming from? Who is buying them? Who is shipping them? How many are captured USA vehicles? What proportion? Potential Tclers: When you get tired of looking at devoid-of-common-sense TV-interviews-with-politicians-and-the-like, try installing-using-changing-enhancing the following Tk GUI script. To help out in making scripts like this, here is a page that provides sources of Tcl-Tk code snippets by providing links to various 'tkGooies' scripts that can make it relatively quick work to compose widget definitions, bind statements, and procedure code. And when you get to the testing-and-debugging phase in development of a Tk script, here is a page that describes the wonderfulness of the 'wish' 'stack trace' facility, which can make the testing-and-debugging go relatively quickly and painlessly. The Tcl-Tk Script CODE Here is a link to CODE for the Tk script 'tkCircleChord_SubtendingAngleAtCenter IsTwiceAngleAtCircumference.tk'. With your web browser, you can 'right-click' on this link --- and in the menu that pops up, select an option like ' Save Link Target As ... ' to save this file to your local computer. Then you can rename the file to remove the '.txt' suffix. Make sure that you have execute permission set on the file --- in order to execute the script.

Some possible FUTURE ENHANCEMENTS There are quite a few enhancements that could be considered for this script, such as: As the chord or point C is moved, display the values of angles A and C: Given that the image is so quickly redrawn when the 'ReDraw' proc is executed, it appears that it should be possible to delete-and-redraw the angles as a point is moved via a 'scale' widget --- and it should be possible to show, on the canvas, the values of the 2 changing angles. Put more observations directly on the canvas or message line : The computations of the two angles, showing that the 'central' angle is indeed always twice the value of the 'inscribed' angle, is 'buried' on the 'ShowState' report. It would probably be more user-friendly to expose the lengths of the sides of the angles directly on the GUI --- somehow (on the canvas or in a label widget). It would also be nice to 'expose' (on the GUI) the way that those lengths are used to calculate the values of angles A and C. 'WritePDFfile', 'WriteGIFfile', 'WritePNGfile' options: Adobe Postscript is becoming a rather obsolete format for exchanging documents with others. The Adobe PDF (Portable Document Format) format is used nowadays, rather than Postscript, for that purpose. Although Tk provides only the Postscript format as an output format for lines and text drawn on a Tk canvas with 'create line', 'create oval', and 'create text' canvas-commands, we could use a utility command like 'ps2pdf' to create a (color) PDF file from a (color) Postscript file. Furthermore, we could use the ImageMagick 'convert' command to convert a color Postscript file to a color GIF file or a color PNG file. More information in the 'ShowState' or 'Help' text display options: There is almost surely some improvements or additions that could be made to the text that I initially provide in the 'ShowState' or 'Help' options. The bottom line here is that there are almost always non-trivial enhancements (or 'forks') that could be made to (or from) a Tk GUI 'app' like this. One advantage of this Tk script is that it is 'open' code --- available to anyone for enhancement. So if you would like to take a different approach to implementing this script, you are welcome to take this code and build on it (or reconstruct it). IN CONCLUSION As I have said on other code-donation pages on this site ... There's a lot to like about a utility that is 'free freedom' --- that is, no-cost and open-source so that you can modify/enhance/fix it without having to wait for someone else to do it for you (which may be never). A BIG THANK YOU to Ousterhout for starting Tcl-Tk, and a BIG THANK YOU to the Tcl-Tk developers and maintainers who have kept the simply MAH-velous 'wish' interpreter going.

Bottom of this web page for presenting Tcl-Tk code for 'tkCircleChord_ TheSubtendingAngleAtCenter_Is_ TwiceTheAngleAtCircumference' --- a Tk-GUI script 'app' in the FE 'tkGooies' system, in the 'MATHed' subgroup of the 'MATHtools' group. To return to a previously visited web page location, click on the Back button of your web browser a sufficient number of times. OR, use the History-list option of your web browser. OR ... < Go to Top of Page, above. > Page history: This FE web page was created 2017 Jan 09. Page was changed 2019 Mar 05. (Added css and javascript to try to handle text-size for smartphones, esp. in portrait orientation.) Page was changed 2019 Jul 03. (Specified image widths in percents to size the images according to width of the browser window. Also added some web links.) NOTE: This code and description has not been posted on a Tcler's Wiki page --- at wiki.tcl-lang.org --- formerly wiki.tcl.tk. If I ever do so, as a backup and alternative to this page, I plan to add a link to that Wiki page here.