FE 'tkGooie' Utilities
'ODEtools' group
|
FE tkGooie interface to simulate a pendulum --- even a wide-swinging one. Larger, hi-res image is below. |
FE Home Page >
FE Downloads Page >
FE 'tkGooies' Description Page >
FE 'tkGooies' 'MATHtools' Page >
FE 'tkGooies' 'ODEtools' Page >
This
'tkSimulateSinglePendulumNoFriction'
tkGooie Page
|
INTRODUCTION to Tcl-Tk script For at least 5 years now (about 2011 to 2016), I have had it on my Tk-scripts-to-do list to implement a GUI that performs numerical-integration of the ODE's (ordinary differential equations) that describe some dynamic physics configurations of classical mechanics --- such as the differential equations describing the angular displacement (and velocity), over time, of an oscillating pendulum. To start off relatively simply, I wanted to simulate a single pendulum suspended from a fixed pivot-point (Wikipedia link). But I wanted to allow for simulating the motion of a wide-swinging pendulum --- which means doing numerical integration of a nonlinear differential equation --- of the form |
D(D(u)) = -g/L * sin(u)
where D represents the time-derivative operator d/dt,
and t represents the time independent variable,
and u represents the angular displacement of the
pendulum arm from vertical,
and g is the acceleration due to gravity (on Earth or
the Moon or Mars or a mountain-top or whatever),
and L is the length of the pendulum arm (the distance
to a heavy mass at the end of the arm, where
the mass is so great that the weight of the
arm is negligible --- or L is the distance
from the fixed-pivot-point to the center-of-mass
of the arm and the mass at the end of the arm).
|
It has been well-known for more than two hundred years (with credits going to Galileo, Huygens, Newton, Leibniz, the Bernoulli's, Euler, and others for early quantitative observations on pendulums) that if you restrict your attention to a pendulum whose swinging is restricted to a small angle --- for example, by displacing the pendulum bob a small angle from its lowest position and letting go --- then the following differential equation can be used to approximate the motion of the pendulum that is oscillating with a 'gentle' swing.
D(D(u)) = -g/L * u
And it became well known that the general solution of this 'linear' equation can be written in the form A * sin(w*t) + B * cos(w*t) where the coefficient w = sqrt(g/L) and where the constants A and B can be determined from two initial conditions (inital angular displacement and initial angular velocity).
I am using 'sqrt' to denote the square root function.) '2pi/w' is the period, T, of the oscillation, where T is in units like seconds per cycle. The reciprocal of T is the cycles per second --- the frequency. So the frequency, f, is 1/T = w/2pi. Thus the solution can be written A * sin(2pi*f*t) + B * cos(2pi*f*t) or A * sin(2pi*t/T) + B * cos(2pi*t/T) An expression of the form A * sin(k*t) + B * cos(k*t) can be written in the form C * sin(k*t + D) where the constant D is called a 'phase angle'. Hence the solutions to the 'linear' pendulum equations are sinusoidal. And one can expect the solutions to the more general 'nonlinear' equations to be similar to sinusoidal functions. But there is no 'nice' math expression for the general solutions to the nonlinear problem --- for example, in terms of (a finite number of) trigonometric functions or polynomials. So, in this Tk GUI utility, we use numerical integration to generate solutions to the 'nonlinear' differential equation --- at discrete points in time. GOALS for the GUI I had the following goals in mind for the GUI. The GUI should allow the user to enter various values for g and L. (Note that the equation for angular acceleration does not involve mass --- the mass factors cancelled out during derivation of the equation. So the angular motion of the friction-less pendulum should be the same whether the mass is 10 kg or 20 kg, for example.
Bottom line: The GUI should also allow the user to enter parameters for the solver process:
AND --- following a solution run, the GUI should also allow the user to start (and stop) an animation of a pendulum drawn on a Tk canvas. The animation is to be shown on a square Tk 'canvas' widget by using 'create line' and 'create oval' and 'delete' commands on the Tk canvas. --- To evaluate any further requirements that we may need for the GUI, it is helpful to know some of the details of
Some details follow. METHOD - MATH MODELLING OF THE PENDULUM MOTION : To make the problem compatible with numerical integration methods, we convert the single 'second order' differential equation D(D(u)) = -g/L * sin(u) to two 'first order' differential equations with u (= u1 = displacement) and D(u) (= u2 = velocity) being functions of t to be generated by integrating these 2 'first-order' differential eqns:
D(u2) = -g/L * sin(u1) starting at initial conditions u1=A and u2=B, where A is an initial angle and B is an initial angular velocity. The common way of expressing these kinds of systems of first order differential equations in compact, general form is D(u) = f(t,u) where u and f are N-dimensional vectors. This is a compact way of expressing a system of scalar differential equations:
D(u1) = f1(t,u1,...,uN) In the case of these pendulum equations, N=2, and we can think of solving for the unknown function vector (u1(t),u2(t)) where the right-hand-side (RHS) of the two scalar pendulum differential equations above can be thought of as a special case of a more general user-specified function vector (f1(t,u1,u2),f2(t,u1,u2)) where
f1(t,u1,u2) = u2
We use the popular Runge-Kutta 4th order method (RK4) to perform the numerical integration for a user-specified time step, h. We basically use two procs to perform the integration steps:
The latter proc ('deriv', say) is called several times by the former proc ('rk4', say), for each time step. METHOD - PLOTTING THE ANIMATION ON THE TK CANVAS : After a solution, we have the solution functions u1 and u2 for a sequence of (equally-spaced) time values. We could use a more complex Runge-Kutta method --- such as Runge-Kutta-Fehlberg --- to get a solution with potentially unequally-spaced time values. 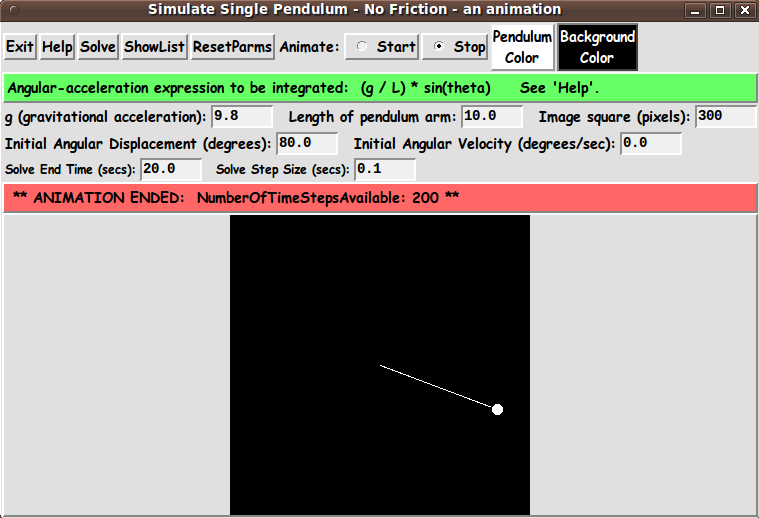We use function u1 (angular displacement) to do the animation. For each time value, t(i), the pendulum is drawn as a simple
Our GUI provides 2 buttons by which the user can specify 2 colors for:
An 'animate' proc performs the pendulum animation when the user clicks on a 'Start' radiobutton of the GUI. This 'animate' proc uses the 'world-coordinates' --- the values of angle u1 --- to draw the swinging pendulum within an square area of about 2*L by 2*L in world coordinates, where L is the length of the pendulum arm. We think of the pivot-point of the pendulum as being at the origin --- (0.0,0.0). We use the angle u1 to compute the x,y coordinates of the end of the pendulum arm (and center of the mass, represented by a circle). The 2Lx2L area allows for the pendulum to swing to extremes:
A proc is provided which maps the plot area limits in world coordinates --- say
UpperLeftCorner: (-L,+L) to the corners of the plot area in pixel coordinates:
UpperLeftCorner: (0,0) We use a value a little larger than L for the world coordinate limits --- to allow for a little margin around the swinging pendulum. To get a square image area, we use ImageWidthPx=ImageHeightPx and we determine this number of pixels by allowing the user to specify the integer value in an entry widget on the GUI. The 'animate' proc uses 2 procs --- 'Xwc2px' and 'Ywc2px' --- to convert the world coordinates of each point --- such as the end-point(s) of the pendulum arm --- to pixel coordinates. The pixel-coordinates are used in the 'create line' and 'create oval' commands to redraw the pendulum-arm and mass (represented by a circle) for each time step. 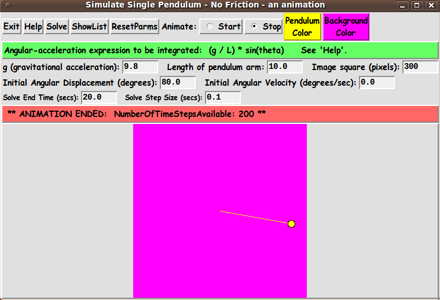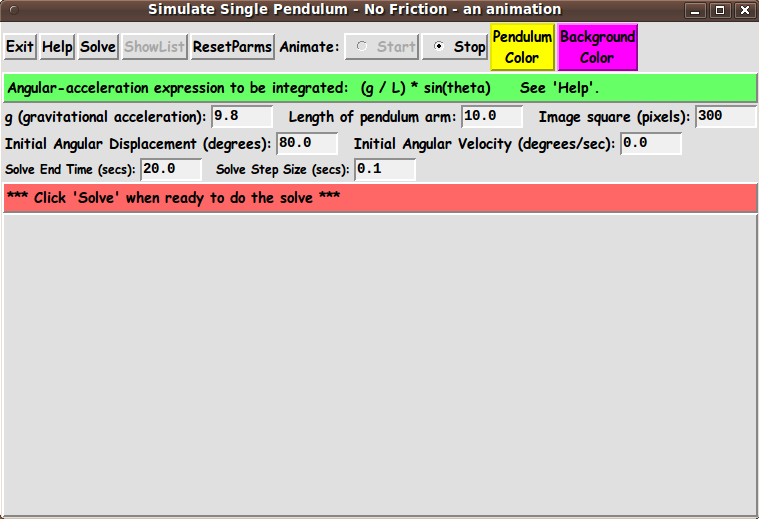THE GUI LAYOUT : Based on the notes above, the Tk GUI should allow the user to specify
There is to be a 'Solve' button to perform a solution when the user is ready to use these parameters. A 'ShowList' button can be used to show the list of solution values --- triplets t(i), u1(t(i)), u2(t(i)) --- in a popup window. We allow the user to specify the two intial values in degrees, rather than radians --- initial angular displacement in degrees and initial angular velocity in degrees/sec. These two values are converted to radians for easy and efficient use in the Tcl sin() function of the solve process. We can add 2 columns to the list output, to show u1 and u2 in degrees, as well as in radians. There are 2 buttons on the GUI by which to call up an RGB-color-selector GUI with which to specify the 2 colors for the animation drawing on the canvas. In addition, on the GUI, there are 'Start' and 'Stop' radiobuttons to start and stop an animation run. --- To allow the user to speed-up or slow-down the animation, there could be a Tk widget ('entry' or 'scale') by which to specify a wait-time (in millisecs) between computing and displaying each new pendulum position. This would be an alternative to using a wait-time value computed according to the solution step-size, h --- which is set by the user, in an 'entry' widget on the GUI. For now, we may simply calculate the animation wait-time based on the time-step, h. --- One way the user can specify all these parameters is indicated by the following 'sketch' of a layout for the GUI. In the following sketch of the GUI: |
SQUARE BRACKETS indicate a comment (not to be placed on the GUI).
BRACES indicate a Tk 'button' widget.
UNDERSCORES indicate a Tk 'entry' widget.
A COLON indicates that the text before the colon is on a 'label' widget.
CAPITAL-O indicates a Tk 'radiobutton' widget.
CAPITAL-X indicates a Tk 'checkbutton' widget (if any).
Vertical bars (and horizontal hyphens) outline a 'canvas' widget.
If there are scrollbars:
Less-than and greater-than signs indicate the left and right ends of a horizontal 'scrollbar'.
Capital-V and Capital-A letters indicate the bottom and top ends of a vertical 'scrollbar'.
Here is the sketch:
FRAMEnames
VVVVVVVVVV
------------------------------------------------------------------------------------------
Simulate Single Pendulum -- No Friction - an animation
[window title]
------------------------------------------------------------------------------------------
.fRbuttons {Exit} {Help} {Solve} {Show {Reset Animate: O Start O Stop {Pendulum {Background
List} Parms} Color} Color}
.fRrhs [ ........ Angular acceleration expression goes here, in a label widget .......... ]
(This could be an entry widget, someday, to allow for changes in the math expression.)
.fRparms g (gravitational acceleration): 9.8__ Length of pendulum arm: 10.0__ Image square (pixels): 300__
.fRinit Initial Anglular Displacement (degrees): 8.0__ Initial Angular Velocity (degrees/sec): 0.0___
.fRtimes Solve End Time (secs): 20.0__ Solve Step Size (secs): 0.005__
.fRmsg [ .......... Messages go here, in a label widget .......................... ]
.fRcanvas |------------------------------------------------------------------------|
| |
| |
| [This area is to contain a non-scrollable square canvas widget |
| in which the animation is to be drawn. |
| |
| The square canvas widget is centered at the top of this area.] |
| |
| |
| |
| |
|------------------------------------------------------------------------|
|
GUI components: From the GUI 'sketch' above, it is seen that this GUI layout consists of about
The GUI (a screenshot) To implement this Tk GUI script, I fetched one of my Tk scripts that had most of these GUI elements and converted it to this 'tkSimulatePendulumNoFriction' script. I ended up with the GUI seen in the following image. |
|
This is the GUI as it first appears. As the message in the middle of the GUI indicates, the user can take the defaults for all the parameters and simply click on the 'Solve' button to do the numerical integration. The first time I ran the solve-process (after fixing a bunch of syntax errors in the code), I was astonished at how quickly the solve completes --- in a fraction of a second! A 'solve completed' message appeared in the message area so quickly after I clicked on the 'Solve' button, I thought that the code did not execute all the mathematical operations for all the time steps. The 'SOLVE DONE' message said that the elapsed time for the solve was 60 milliseconds --- less than one-tenth of a second for 200 time-steps of integration. Not bad, considering I have not expended time trying to obtain the optimum speed out of all the numerical integration code. When I clicked on the 'ShowList' button, a list of the computed results --- time, angular-displacement in radians, angular-velocity in radians per second, angular-displacement in degrees, angular-velocity in degrees per second --- appeared for the 200 time steps and corresponded to the default initial conditions. --- Note that you can use the 'ShowList' button to generate columns of decimal numbers that can be copied-and-pasted into a text-editor window. The text editor can be used to save the data to a text file. Then that text file can be edited (to remove or comment out the header and trailer text) and fed into a 'tkGooie' XY-function plot utility such as to get a plot of the displacement and velocity functions (in radians or degrees). --- To give you an idea of what the animation image area looks like, here is a 'screenshot'. |
|
Before clicking the 'Start' button for this animation, I used the 2 color buttons to call up a color selector GUI to set the pendulum color to white and the background color to black. The reduced-size screenshot at the top of this page shows the image area in the default colors --- yellow for the pendulum arm-and-mass and magenta for the background. --- HELP TEXT The 'Help' button on the GUI shows extensive text describing this utility, in a popup window with scrollbars for the text area. DESCRIPTION OF THE CODE Below I provide a link to the Tk script code for this 'tkSimulatePendulumNoFriction' utility. For this Tk script, I follow my usual 'canonical' structure for Tk code: |
0) Set general window & widget parms (win-name, win-position,
win-color-scheme, fonts, widget-geometry-parms, win-size-control,
text-array-for-labels-etc).
1a) Define ALL frames (and sub-frames, if any).
1b) Pack ALL frames and sub-frames.
2) Define & pack all widgets in the frames, frame by frame.
Within each frame, define ALL the widgets. Then pack the widgets.
3) Define keyboard and mouse/touchpad/touch-sensitive-screen action
BINDINGS, if needed.
4) Define PROCS, if needed.
5) Additional GUI initialization (typically with one or more of
the procs), if needed.
|
This Tk coding structure is discussed in more detail on the page A Canonical Structure for Tk Code --- and variations. This structure makes it easy for me to find code sections --- while generating and testing a Tk script --- and when looking for code snippets to include in other scripts (code re-use). I call your attention to step-zero. One thing that I started doing in 2013 is using a text-array variable --- named 'aRtext' --- for text in labels, buttons, and other widgets in the GUI. This can make it easier for people to internationalize my scripts. I will be using a text-array like this in most of my scripts in the future. Experimenting with the GUI As in all my scripts that use the 'pack' geometry manager (which is all of my 100-plus scripts, so far), I provide the four main 'pack' parameters
on all of the 'pack' commands for the frames and widgets. That helps me when I am initially testing the behavior of a GUI (the various widgets within it) as I resize the main window. I think that I have used a nice choice of the 'pack' parameters. In particular ... The labels and buttons and entry widgets stay fixed in size and relative-location as the window is re-sized --- while the area containing the 'canvas' can expand/contract as the window is re-sized. You can experiment with the '-side', '-anchor', '-fill', and '-expand' parameters on the 'pack' commands for the various frames and widgets --- to get the widget behavior that you want. --- Additional experimentation with the GUI: You might want to change the fonts used for the various GUI widgets. For example, you could change '-weight' from 'bold' to 'normal' --- or '-slant' from 'roman' to 'italic'. Or change font families. In fact, you may NEED to change the font families, because the families I used may not be available on your computer --- and the default font that the 'wish' interpreter chooses may not be very pleasing. I use variables to set geometry parameters of widgets --- parameters such as border-widths and padding. And I have included the '-relief' parameter on the definitions of frames and widgets. Feel free to experiment with those 'appearance' parameters as well. --- Note that the color buttons call on a color-selector-GUI script to set the colors. You can make that color-selector script by copying-and-pasting the code from the page offering 'a non-obfuscated color selector GUI', on this site. Some comments and code at the bottom of this 'pendulum animation' Tk script explain how you can implement the RGB color selector script. Some features in the code There are plenty of comments in the code, to describe what most of the code-sections are doing. You can look at the top of the PROCS section of the code to see a list of the procs used in this script, along with brief descriptions of how they are called and what they do. --- Here is a brief overview of the procs of the script. |
- 'solve' - called by the 'Solve' button.
- 'runge-kutta-4' - called by the 'solve' proc.
- 'deriv' - called by the 'runge-kutta-4' proc.
- 'show_list' - called by the 'ShowList' button
- 'animate' - called by a click on the 'Start' animation radiobutton.
- 'setMappingVars_for_px2wc' - called by proc 'animate'.
- 'Xwc2px' - called by proc 'animate'.
- 'Ywc2px' - called by proc 'animate'.
- 'set_pendulum_color1' - called by the 'PendulumColor' button.
- 'set_background_color2' - called by the 'BackgroundColor' button.
- 'update_color_button' - sets background & foreground color of
either of the 2 color buttons ---
called by the 2 'set_*_color*' procs and in the
'Additional GUI Initialization' section,
to initialize colors on the 2 color buttons.
- 'advise_user' - called by the 'solve' and 'animate' procs.
- 'reset_parms' - called by the 'ResetParms' button and in the
'Additional GUI Initialization' section,
to initialize the parms.
- 'edit_inputs' - called by 'solve' and 'animate' procs
- 'decimal_check' - called by 'edit_inputs' proc
- 'popup_msgVarWithScroll' - called by the 'Help' button.
|
The main numerical integration code is in the 'runge-kutta-4' and 'deriv' procs. See the comments in those procs for details on their implementation. A fervent hope It is my hope that the copious comments in the code will help Tcl-Tk coding 'newbies' get started in making GUI's like this. Without the comments, potential young Tcler's might be tempted to return to their iPhones and iPads and iPods --- to find
A recent (2016) poll asked people whether they preferred
13 percent of the respondents opted for the meteor strike. That would be my vote too. But if that happens, then all my work on these Tk scripts will be for naught --- unless the insects that survive the strike evolve into beings with advanced intellect who manage to learn to read the digital and paper text remnants that might survive the meteor strike --- and re-invent computers and Tcl-Tk. The Tcl-Tk CODE : Here is a link to CODE for the script 'tkSimulateSinglePendulumNoFriction.tk'. With your web browser, you can 'right-click' on this link --- and in the menu that pops up, select an item like 'Save Link Target As ...' --- to save this file to your local computer. Then you can rename the file to remove the '.txt' suffix. Make sure that you have execute permission set on the file --- in order to execute the script. SOME POTENTIAL ENHANCEMENTS: I ran across a document on differential equations that presented a table that summarizes some of the single-pendulum problems and their second-order differential equations. The table looked like this:
(The damping is linear in these.) This table suggests some features that I may add to this Tk script --- or implement in a separate Tk script:
--- There will probably more enhancements that I may think of in the future. But some enhancements might be more suitable for putting in a separate Tk script using somewhat different equations or GUI design or methods. --- For those who might want to go ahead and add enhancements: To help out in making Tk scripts like this, here is a page that provides sources of Tcl-Tk code snippets by providing links to various 'tkGooies' scripts that can make it relatively quick work to compose
And when you get to the testing-and-debugging phase in development of a Tk script, here is a page that describes the wonderfulness of the 'wish' 'stack trace' facility which can make the testing-and-debugging go relatively quickly and painlessly. IN CONCLUSION There's a lot to like about a utility that is 'free freedom' --- that is, no-cost and open-source so that you can modify/enhance/fix it without having to wait for someone else to do it for you (which may be never). I hope to provide more free scripts that can be used to demonstrate mathematical and physics principles (and Tk coding techniques) --- scripts that could be used in a classroom or self-teaching setting. As I have said on other 'tkGooie' pages of this FE web site ... A BIG THANK YOU to Ousterhout for starting Tcl-Tk, and a BIG THANK YOU to the Tcl-Tk developers and maintainers who have kept the simply MAH-velous 'wish' interpreter going. |
|
Bottom of this page fo
To return to a previously visited web page location, click on the
Back button of your web browser a sufficient number of times.
OR, use the History-list option of your web browser.
< Go to Top of Page, above. >Page history:
This FE web page was created 2016 Jul 07.
NOTE: |