FE 'tkGooies' Utilities 'MATHed' subgroup of the 'MATHtools' group Tk-GUI script 'tkVarignonsTheorem' (Code for a GUI to demonstrate that the midpoints of the sides of ANY quadrilateral make a parallelogram) (FE = Freedom Environment)

GUI which allows the user to drag the vertices of the quadrilateral and watch that the midpoints always determine a parallelogram.

FE Home Page > FE Downloads Page >

FE 'tkGooies' Description Menu >

FE 'tkGooies' 'MATHtools' Menu >

FE 'tkGooies' 'MATHed' Menu >

This
'tkVarignonsTheorem'
tkGooie code Page

INTRODUCTION to Tcl-Tk script 'tkVarignonsTheorem' For several years (circa 2013-2015), I had been planning to make various 'Math Education' Tk GUI's that illustrate various discoveries that have been made through the ages --- in plane geometry, number theory, etc. In the 2013-2016 time frame, I started making a few 'tkGooies' of these types: Thales' Theorem: Triangle Inscribed in a Semicircle is always Right Triangle An Eratosthenes Prime Sieve (pixels in a resizable canvas) Approximating Circle Circumference By Polygons (a demonstration of Archimedes' method) In my readings of various books popularizing math and, in particular, books containing discoveries in plane (Euclidean) geometry, I ran across static images that demonstrate Varignon's Theorem --- the fact that if you connect the midpoints of the 4 sides of ANY quadrilateral, the resultant quadrilateral is a parallelogram. You can see some such images on the Wikipedia page on Varignon's Theorem --- a theorem attributed to Pierre Varignon who died in 1722. That theorem was post-humously published in 1731 in a collection of his lectures. (I am rather surprised that nobody, in the 2000 years during which Euclid's 'Elements' had been widely circulated, was known to have commented on this phenomenon. Of course, it is not easy to explore what happens with the midpoints of a quadrilateral without doing a lot of tedious drawings --- or manufacture a device to demonstrate this 'feature' of quadrilaterals and midpoints.) If you want more information on Varignon and his discovery about quadrilaterals and midpoints and parallelograms, you can do a WEB SEARCH on keywords like 'varignon quadrilateral midpoint parallelogram' If you can deal with the annoying popups and advertisements, one web site that is rife with math results is the 'Cut The Knot' site --- which has a page on Varignon's Theorem. In any case, with the Tk script (whose code is presented on this page), I was seeking to make the demonstration of Varignon's Theorem an interactive and dynamic, animated experience --- using Tcl-Tk. Around 2016, with the advent of Javascript enhancements associated with HTML 3.0, some dynamic, interactive demos of math results started appearing on the internet, such as the 'Wolfram Demonstrations Project' which included a page on 'The Midpoint Quadrilateral Theorem' --- giving the theorem a descriptive name in place of Varignon's name. One feature of the 'tkGooie' presented on this page is that it comes bundled within a 'tkGooies' menu-driven system that can be installed on a computer --- or on a file server that serves files to multiple computers. Another feature of the 'tkGooies' is that I generally provide more control of colors than one sees in many math demo utilities. 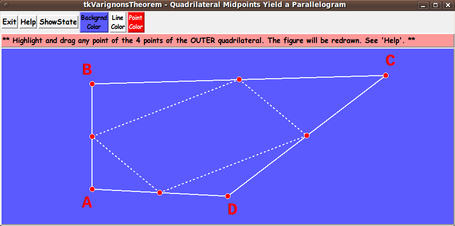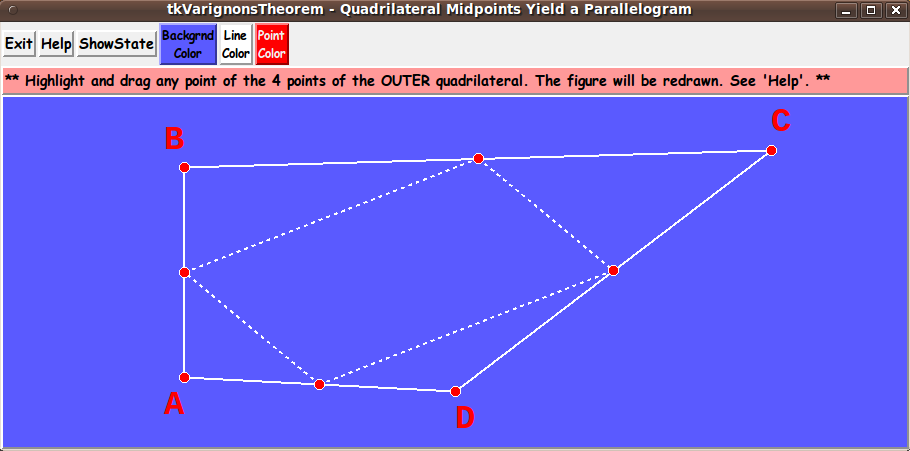Basic Goals of the Tk Script: My purpose for this Tk GUI script is/was to generate a quadrilateral and its midpoints --- and connect the midpoints with straight line segments. The drawings are to be done in a resizable rectangular image area --- in a Tk 'canvas' widget. 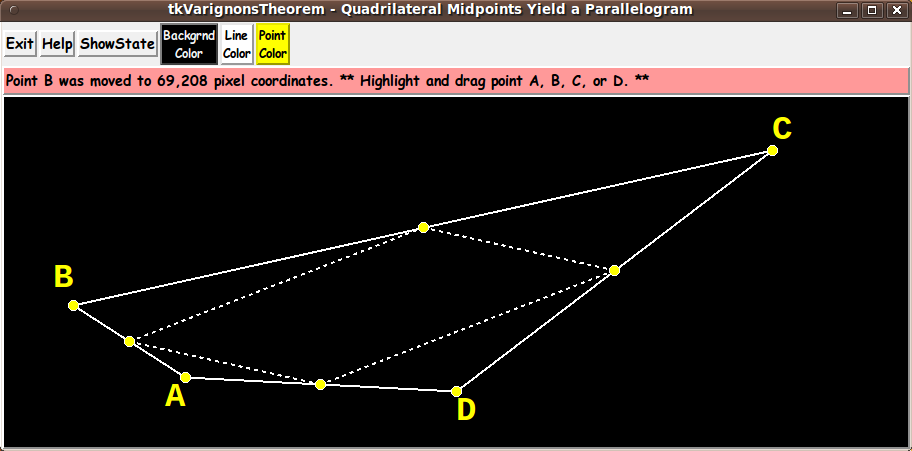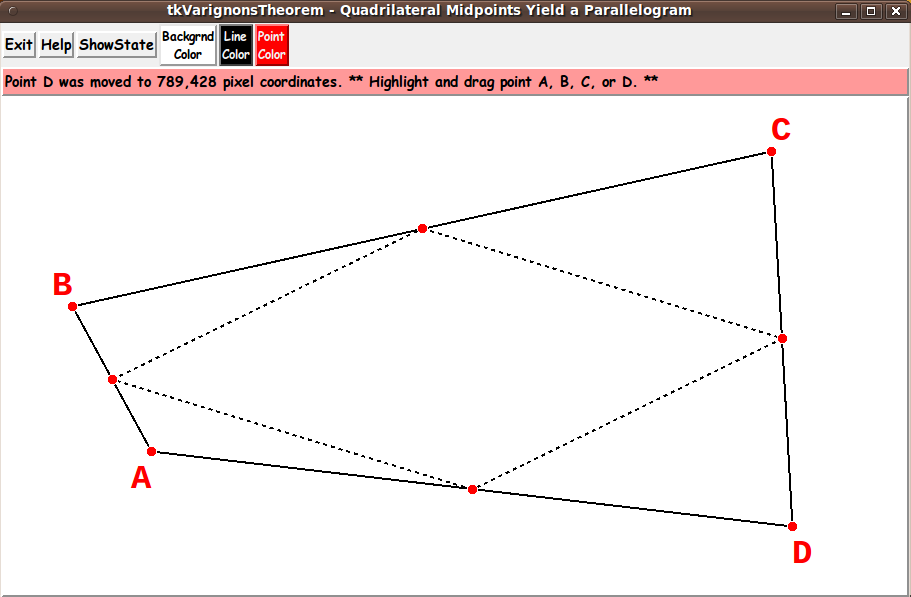The GUI is to allow the user to drag the 4 corners (vertex points) of the 'outer' quadrilateral. And the GUI is to automatically delete-and-redraw (for the user) any changed midpoints --- and delete-and-redraw the resulting parallelogram. PLANNED LAYOUT OF THE GUI: As I have done with other Tk scripts that I have written in the past year or so, I laid out a 'text image' of the GUI --- to aid me as I coded the frames and widgets. I used the following conventions to make the sketch, with a text editor.

  SQUARE-BRACKETS indicate a comment (not to be placed on the GUI).
  BRACES          indicate a Tk 'button' widget.
  A COLON         indicates that the text before the colon is on a 'label' widget.
  <---O--->       indicates a Tk 'scale' widget (if any).
  CAPITAL-X       indicates a Tk 'checkbutton' widget (if any).
  CAPITAL-O       indicates a Tk 'radiobutton' widget (if any).
  UNDERSCORES     indicate a Tk 'entry' widget (if any).


  According to those conventions,
  I created the following 'text sketch'.


 FrameNames
 VVVVVVVVVV
              -----------------------------------------------------------------------------
              tkVarignonsTheorem
              [window title]
              -----------------------------------------------------------------------------

 .fRbuttons   {Exit} {Help} {ShowState} {Backgd  {Line   {Point
                                         Color}   Color}  Color}
 
 .fRmsg       [ .......... Message line --- for advice to the user .................. ]

 .fRcanvas    -----------------------------------------------------------------------------
              |                                                                           |
              |                                                                           |
              |                                                                           |
              |  [Canvas for displaying the two quadrilaterals                            |
              |   in a rectangular image area. No scrollbars.]                            |
              |                                                                           |
              |                                                                           |
              |                                                                           |
              |                                                                           |
              -----------------------------------------------------------------------------

Perhaps some aspects of the sketch could use a little more explanation:

  A combination of VERTICAL-BAR CHARACTERS AND HYPHEN (or UNDERSCORE) CHARACTERS,
  that outline a RECTANGULAR SHAPE, are used to indicate either a Tk 'canvas' or
  a Tk 'listbox' widget or a Tk 'text' widget.

  A LINE (HYPHENS or VERTICAL-BARS) WITH AN 'ARROW-HEAD' AT EACH END indicates
  a Tk 'scale' widget --- or a 'scrollbar' widget.

  SCROLL-BAR 'ARROW-HEADS' (for a 'canvas', 'listbox', or 'text' Tk widget)
  are drawn as follows:

   UP    ARROW-HEAD   is drawn with a CAPITAL-A.
   DOWN  ARROW-HEAD   is drawn with a CAPITAL-V.
   LEFT  ARROW-HEAD   is drawn with a LESS-THAN sign.
   RIGHT ARROW-HEAD   is drawn with a GREATER-THAN sign.

  UP-and-DOWN    ARROW-HEADS  at the right/left of a box shape indicate
  a VERTICAL SCROLL-BAR there.

  LEFT-and-RIGHT ARROW-HEADS  at the bottom/top of a box shape indicate
  a HORIZONTAL SCROLL-BAR there.

  The arrow-heads on a horizontal scrollbar are joined by hyphens, rather than
  underscores.

From the diagram above, I could see that this GUI will contain about: 6 'button' widgets 1 'label' widget 1 'canvas' widget (with no x-y scrollbars) 0 'entry' widgets 0 'checkbutton' widgets 0 'radiobutton' widgets 0 'scale' widgets 0 'listbox' widgets 0 'text' widgets Assembling the pieces (The GUI) Now it was a matter of putting the pieces together. I took 'code-pieces' from some of my other Tk scripts that 'draw' in an image area on a Tk canvas. I ended up with the following GUI as an initial display.

Note that I have provided 3 color buttons on the GUI so that the user can control : the background color of the image area the color of the line-segments of the quadrilateral and parallelogram the color of the vertex points of the quadrilateral and parallelogram --- as well as the color of text-characters that label the vertices. The message line just below the color-buttons indicates that the user can drag any of the 4 corner-points (A,B,C,D) of the 'outer' quadrilateral. By default, the GUI starts with an initial quadrilateral --- and uses the midpoints of its sides to draw the resulting parallelogram. A 'ShowState' button at the top of the GUI displays a popup text window that contains numerical information: coordinates of the 'outer' quadrilateral (in 'pixel units') coordinates of the midpoints (in 'pixel units') lengths of the sides of the 'outer' quadrilateral (in 'pixel units') length of the sides of the parallelogram (in 'pixel units') --- which shows that the opposite sides are of equal length, and thus confirms that the quadrilateral connecting the midpoints is indeed a parallelogram. --- Below is an image that was drawn after dragging vertex B to the left and down. In addition, the background color was changed to black, and the color of the colored-disks representing the points (and the text labelling the points) was changed to yellow.

And below is an image drawn after enlarging the 'canvas' area by dragging the lower-right corner of the GUI window. After enlarging the canvas, the point D was dragged down and to the right. In addition, the background color was changed to white, the color of the line segments was changed to black, and the color of the colored-disks representing the points (and their text) was changed back to red. Note that you may want to change the canvas background to white if you are going to capture the image and print it to a printer. This will save a lot of ink.

Execution time: After dragging a vertex (A,B,C, or D), the computations and drawing complete almost immediately after completing the drag (releasing the mouse-button, for example). Wouldn't Varignon (and Euclid and Archimedes and Galileo and Newton and Euler and the Bernoulli's and Gauss and Lagrange and Laplace and Weierstrass and Poincare and Riemann and ...) have loved to be able to use Tcl-Tk? I wonder what wonders Varignon et. al. would have performed with the 'wish' interpreter at their disposal? Sure beats drawing in the sand or drawing with quill and ink-well. --- Distance units When I started writing this script, I considered specifying the coordinates of the various (eight) points in 'world coordinates' --- and then mapping those coordinates to pixel coordinates --- as I have done in other geometry 'tkGooies' such as Approximating Circle Circumference By Polygons (a demonstration of Archimedes' method) But the user does not need to be aware of an origin and a coordinate system when dragging the points. So I decided to perform all the computations within the script based on 'pixel coordinates' rather than 'world coordinates'. Hence, the 'ShowState' option shows all point locations and length computations in 'pixel coordinates'. --- Implementing the Color Buttons The 3 color buttons call on an 'external' color-selector-GUI script to set those colors. You can make that color-selector script by cutting-and-pasting the code from the page that offers a non-obfuscated color selector GUI on this site. You can see the code at the bottom of this 'tkVarignonTheorem' script to see how the name and location of the color selector script is set. DESCRIPTION OF THE CODE Below, I provide the Tk script code for this 'tkVarignonTheorem' 'app'. I follow my usual 'canonical' structure for Tk code, for this Tk script:

  0) Set general window & widget parms (win-name, win-position,
     win-color-scheme, fonts, widget-geometry-parms, win-size-control).

  1a) Define ALL frames (and sub-frames, if any).
  1b) Pack   ALL frames and sub-frames.

  2) Define & pack all widgets in the frames, frame by frame.
              Within each frame, define ALL the widgets.
              Then pack the widgets.

  3) Define keyboard and mouse/touchpad/touch-sensitive-screen action
     BINDINGS, if needed.

  4) Define PROCS, if needed.

  5) Additional GUI initialization (typically with one or more of
     the procs), if needed.

This Tk coding structure is discussed in more detail on the page A Canonical Structure for Tk Code --- and variations. This Tk coding structure makes it easy for me to find code sections --- while generating and testing this script, and when looking for code snippets to include in other scripts (code re-use). Experimenting with the GUI As in all my scripts that use the 'pack' geometry manager (which is all of my 100-plus Tk scripts, so far), I provide the four main 'pack' parameters: '-side' '-anchor' '-fill' '-expand' on all the 'pack' commands for the frames and widgets. I think I have found a good setting of the '-side', '-anchor', '-fill', and '-expand' parameters on the 'pack' commands for the various widgets of this GUI. In particular ... The 'canvas' widget will expand/contract appropriately when the GUI window size is changed --- and button and label widgets stay fixed in size and relative-location when the window is re-sized. If anyone wants to change the way the GUI configures itself as the main window size is changed, they can experiment with the '-side', '-anchor', '-fill', and '-expand' parameters on the 'pack' commands for the various widgets --- to get the widget behavior that they want. --- Additional experimentation with the GUI --- its appearance: You could change the fonts used for the various GUI widgets. For example, you could change '-weight' from 'bold' to 'normal' --- or '-slant' from 'roman' to 'italic'. Or change font families. In fact, you may NEED to change the font families, because the families I used may not be available on your computer --- and the default font that the 'wish' interpreter chooses may not be very pleasing. Furthermore, there are variables used to set geometry parameters of widgets --- parameters such as border-widths and padding. And you could change the '-relief' values for frames and widgets. Feel free to experiment with those 'appearance' parameters as well. Some features of the code There are plenty of comments in the code to describe what most of the code-sections are doing. See the top of the 'PROCS' section of the script for a list of the procs used in this Tk script. See comments in the procs for details on the purpose of each proc and for details on the methods by which each proc was implemented. Below is a quick overview of the procs --- to give an idea of the 'guts' of this utility:

    'initDraw'           - This proc is called in the 'Additional GUI
                           Initialization' section at the bottom of this
                           script to put an initial drawing of the original
                           'outer' quadrilateral --- and the 'inner',
                           'mid-points' quadrilateral --- on the canvas.

 The following 3 procs handle moving an 'outer' quadrilateral point
 --- any of the 4 points called A,B,C,D.

   'pointSelect'      - called by a button1-press   binding on an 'outer'-point-tag of the canvas.
   'pointMove'        - called by a button1-motion  binding on the canvas.
   'pointMoveEnd'     - called by a button1-release binding on an 'outer'-point-tag of the canvas.

   'redraw4movedA'    - called by proc 'pointMoveEnd', to delete and redraw the points,
                        lines, and text affected by moving 'outer' point A.
   'redraw4movedB'    - called by proc 'pointMoveEnd', to delete and redraw the points,
                        lines, and text affected by moving 'outer' point B.
   'redraw4movedC'    - called by proc 'pointMoveEnd', to delete and redraw the points,
                        lines, and text affected by moving 'outer' point C.
   'redraw4movedD'    - called by proc 'pointMoveEnd', to delete and redraw the points,
                        lines, and text affected by moving 'outer' point D.

   'show_state'        - reports on the state of the current image:
                            - the coordinates of the 8 points
                            - the lengths of the 8 lines
                         Called by the 'ShowState' button.

 Other utility procs:   

  'set_background_color'    - Sets the color for the canvas (background).
                              Called by the 'BackgroundColor' button.
 
  'set_line_color'          - Sets the color for the circle on the canvas.
                              Called by the 'LineColor' button.
 
  'set_point_color'         - Sets the color for the inscribed polygon.
                              Called by the 'PointColor' button.
                              
  'update_button_colors'    - Sets the color of the 4 color buttons.
                              Called by the 'set_*_color' procs.

  'advise_user'             - Used by various procs to put a message for
                              the user on a message line of the GUI.        

  'popup_msgVarWithScroll'  - called by 'Help' button to show HELPtext var.

The initial drawing on the canvas is performed by the 'initDraw' proc. See the comments in that proc to see how it is implemented. The procs 'pointSelect' and 'pointMove' handle displaying a moving point on the canvas when the user drags any of the 4 points A,B,C,D. The proc 'pointMoveEnd' handles redrawing the figure when the user finishes dragging any of the 4 points A,B,C,D. The proc 'pointMoveEnd' uses proc 'redraw4movedA' or 'redraw4movedB' or 'redraw4movedC' or 'redraw4movedD' to redraw the image on the canvas --- depending on which point was moved. A fervent hope It is my hope that the copious comments in the code might help Tcl-Tk coding 'newbies' get started in making GUI's like this. Without the comments --- especially in the 'initDraw' and 'point*' and 'redraw*' procs --- the code might look even more cryptic than it already is. Without the comments, potential young Tcler's might be tempted to return to their iPhones and iPads and iPods --- to look for videos of TV news organizations interviewing politicians and their 'surrogates' (and NOT asking obvious follow-up questions). Examples: For 'Birthers' who believe Obama was born in Kenya --- a follow-up question that is never asked: Do you really think that Obama's mother would choose to go to Kenya to have her baby born in a hospital there --- rather than stay in Hawaii and have the baby delivered in a hospital in Hawaii --- where both she and her baby were likely to receive better care and a less risky delivery outcome? For 'public open carry' fanatics --- some follow-up questions that are never asked: Do you really think that families with children are going to want to walk around a mall or store with you walking around with a gun on your hip? Do you really think that store owners are going to want you scaring their customers away? (If their answer to the first question is Yes, then ask them if they have children --- or grandchildren. And if their answer is Yes to that, then ask them if they understand why many parents and grandparents would not feel the same way.) And if none of that 'works', then ask them: Do you really think you can trust all those other people carrying around guns that they are not going to use their gun on you --- if you happen to tick them off? For 'arm the teachers' fanatics --- follow-up questions that are never asked: Are you aware that there are many emotionally disturbed students in our public schools? Are you aware that many of those students are violence-prone? Are you aware that many of those students are bigger and stronger than their teachers? Are you aware that a teacher (even a 'trained' one) will not be able to keep a gun in her/his classroom --- day after school day --- from getting in the hands of an outraged, emotionally-disturbed, violence-prone student? For 'open (or concealed) carry on college campuses' fanatics --- follow-up questions that are never asked: Do you really think that a vast majority of parents of college-age children are going to want their children to attend classes or walk around a campus with you walking around with a gun on your hip? Do you really think that most professors at Harvard, Yale, and Stanford (to name a few universities) are going to want you --- or any student --- especially one who just received a bad grade --- sitting in their classrooms or in their offices with a gun on your/their hip? Do you really think that all the students sitting around you in a classroom (you with your gun on your hip) are going to feel comfortable/safe with that? (Don't be surprised if many students drop the class --- or drop out of the university and go to one with different rules, but a reasonably good security system.) Potential Tclers: When you get tired of looking at devoid-of-common-sense TV-interviews-with-politicians-and-the-like, try installing-using-changing-enhancing the following Tk GUI script. To help out in making scripts like this, here is a page that provides sources of Tcl-Tk code snippets by providing links to various 'tkGooies' scripts (and wiki.tcl.tk scripts) that can make it relatively quick work to compose widget definitions, bind statements, and procedure code. And when you get to the testing-and-debugging phase in development of a script, here is a page that describes the wonderfulness of the 'wish' 'stack trace' facility, which can make the testing-and-debugging go relatively quickly and painlessly. The Tcl-Tk Script CODE Here is a link to CODE for the Tk script 'tkVarignonsTheorem.tk'. With your web browser, you can 'right-click' on this link --- and in the menu that pops up, select an option like ' Save Link Target As ... ' to save this file to your local computer. Then you can rename the file to remove the '.txt' suffix. Make sure that you have execute permission set on the file --- in order to execute the script.

Some possible FUTURE ENHANCEMENTS There are quite a few enhancements that could be considered for this script, such as: Provide more numeric results in the 'ShowState' proc: The 'Cut The Knot' math web site has a page on Varignon's Theorem which points out that the area of the parallelogram is ALWAYS half the area of the original quadrilateral. The 'ShowState' proc could be enhanced to compute the areas of the parallelogram and the 'outer' quadrilateral --- to show that one area is always half of the other. Draw the parallelograms as a point is dragged: Given that the image is so quickly redrawn when the mouse-button is released after dragging a point, it appears that it may be possible to delete-and-redraw the parallelograms as a point is dragged. This would amount to putting the calls to the 4 'redraw*' procs into the 'pointMove' proc, instead of only the 'pointMoveEnd' proc. A 'Write-AniGIF' option: If it were desirable to 'record' the points being dragged and the images being redrawn, the GUI could offer an option to write an animated-GIF file (or movie file) from a sequence of images generated from the canvas. It would certainly be more convenient than having to do a bunch of image captures and manually contruct an animated-GIF (or movie) file from a sequence of still-image captures. I have implemented a Write-Ani-GIF option in several 'tkGooies' in the 'IMAGEtools' group, such as: Merge 2 Images Grid-Warp an Image wheeeMorph between two images I can use code from one or more of those Tk scripts to make it relatively easy to implement a Write-Ani-GIF option. The bottom line here is that there are almost always non-trivial enhancements that could be made to --- or 'forks' that could be made from --- a Tk GUI 'app' like this. One advantage of this Tk script is that it is 'open' code --- available to anyone for enhancement. So if you would like to take a different approach to implementing this script, you are welcome to take this code and build on it (or reconstruct it). IN CONCLUSION As I have said on other code-donation pages on this site ... There's a lot to like about a utility that is 'free freedom' --- that is, no-cost and open-source so that you can modify/enhance/fix it without having to wait for someone else to do it for you (which may be never). A BIG THANK YOU to Ousterhout for starting Tcl-Tk, and a BIG THANK YOU to the Tcl-Tk developers and maintainers who have kept the simply MAH-velous 'wish' interpreter going.

Bottom of this web page for presenting Tcl-Tk code for 'tkVarignonsTheorem' --- a tkGooie 'app' in the FE 'tkGooies' system, in the 'MATHed' subgroup of the 'MATHtools' group. To return to a previously visited web page location, click on the Back button of your web browser a sufficient number of times. OR, use the History-list option of your web browser. OR ... < Go to Top of Page, above. > Page history: This FE web page was created 2016 Sep 17. Page was changed 2019 Mar 05. (Added css and javascript to try to handle text-size for smartphones, esp. in portrait orientation.) Page was changed 2019 Jul 03. (Specified image widths in percents to size the images according to width of the browser window. Also added some web links.) NOTE: This code and description has not been posted on a Tcler's Wiki page --- at wiki.tcl-lang.org --- formerly wiki.tcl.tk. If I ever do so, as a backup and alternative to this page, I plan to add a link to that page here.