|
Note that the factor (r * (1 - u/k)) is the effective growth rate.
In this form, the rate goes to zero as the population, u, approaches
the 'saturation level', k.
And the growth rate is about 'r' at very low population levels
that are not triggering the limits to growth.
Note that the factor (1 - u/k) may under-estimate --- or
over-estimate --- the rate at which the growth rate goes to zero as
the population u increases.
That is, the ratio u/k may approach 1 too slowly or too quickly
--- as u increases.
Hence (1 - u/k) may not provide a good prediction of the population in
a given situation --- human population, bacterial population,
or other.
It may be that the factor
(1 - u/k)
should take some other form such as
(1 - (u/k)^2) OR (1 - sqrt(u/k))
to more accurately model the change in population growth rate
as population increases.
There are many other critiques that could be leveled at the
'logistic' ODE --- such as, the 'growth rate at low population
levels' --- 'r' --- is not really a constant.
The 'r' factor would depend on many growth-rate influencers,
such as changes in medical procedures.
So 'r' probably should not be formulated as a constant.
And specifying the population limit 'k' is like putting the
'cart before the horse' --- or 'weighting the dice' to
pre-determine the outcome.
The limit 'k' would depend on many factors,
such as changes in what is acceptable for living conditions.
And 'k' should probably have a more complex form --- and be
made up of many other constants --- such as the size of the
growth area and the amount of certain resources available.
But, for now, we stick with the classic 'logistic' equation.
It gives us a rough idea of how a population could be
expected to increase ---- for given 'r' and 'k', constants.
These considerations demonstrate why the Tk script that I wanted to write
would use numerical integration to solve a differential equation
--- rather than trying for an algebraic 'closed-form' solution to
any differential equation for population growth that might come
under consideration.
A numerical solution method (applied to a differential equation)
will allow for solving a wide variety of forms of the
growth rate equation.
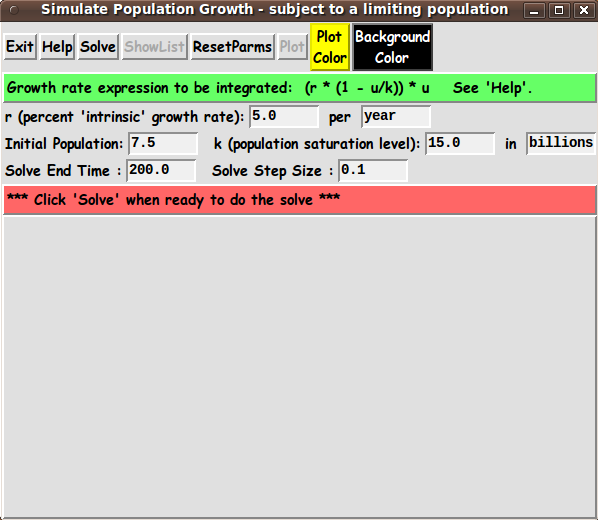
GOALS for the GUI
For now, I decided to go with the 'logistic' differential equation
above.
In that case, the GUI should allow the user to enter various values
for 'r' and 'k'.
The GUI also should allow the user to enter parameters
for the solver process:
-
an initial population level
-
an end-time for the end of the solution process
(where we typically think of time measured in years,
when we are modeling human population growth)
-
a time-step, h, for the solution process,
where h can be a very small fraction of a year.
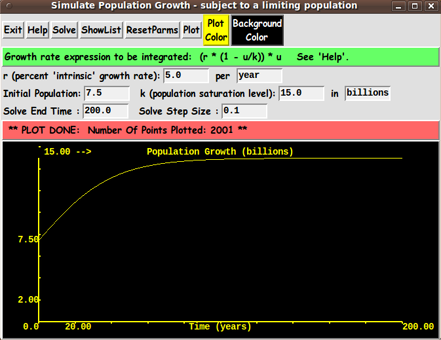
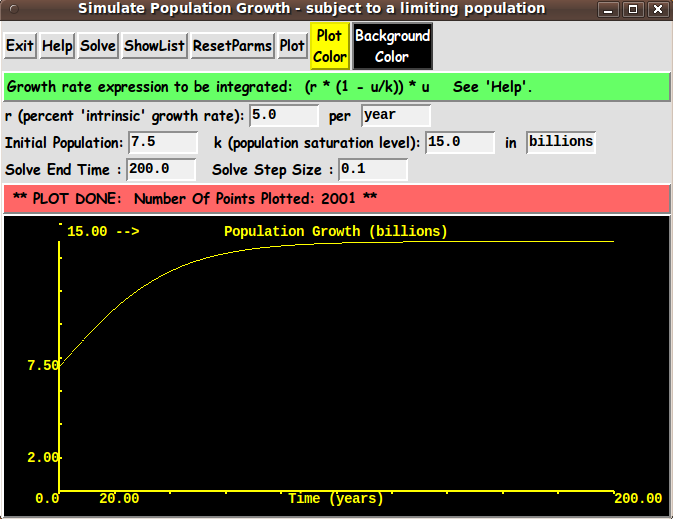
After the data from a solution run is available, the GUI script
could activate a 'Plot' button that allows the user to plot a
graph of the population curve --- drawn on a Tk 'canvas' widget.
The plot is to be drawn on a rectangular Tk 'canvas' widget
by using 'create line' and 'create text'
commands on the Tk canvas.
---
To evaluate any further requirements that we may need for the GUI,
it is helpful to know some of the details of
Some details follow.
METHOD of MATH MODELING OF THE 'LOGISTIC' EQUATION :
We write the first-order non-linear population equation as
D(u) = r * (1 - u/k) * u
with initial condition u(0)=A, where A is an initial population value
(of humans, bacteria, viruses, parasites, ants, roaches, termites,
algae, scum, whatever).
The common way of expressing systems of 'first order'
differential equations in compact, general form is
D(u) = f(t,u)
where u and f are N-dimensional vectors.
This is a compact way of expressing a system of scalar
differential equations:
D(u1) = f1(t,u1,...,uN)
D(u2) = f2(t,u1,...,uN)
. . . . . . . . . . .
D(uN) = fN(t,u1,...,uN)
by letting u be vector (u1, u2, ... , uN)
and
f(t,u) be vector (f1(t,u1,...,uN), ... , fN(t,u1,...,uN))
---
In the case of the 'logistic equation', N is equal to 1.
We can think of solving for the unknown 1-D function vector
(u1(t)) where the right-hand-side (RHS) of the
'logistic' equation above can be thought of as a special
case of a more general user-specified 1-D function vector
(f1(t,u1)) where
f1(t,u1) =
r * (1 - u1/k) * u1 =
r * (u1 - u1^2/k)
which is a 2nd-degree polynomial with respect to variable u1.
We use the popular Runge-Kutta 4th order method (RK4) to
perform the numerical integration for a user-specified
time step, h.
We basically use two procs to perform the integration
steps:
-
a proc to perform the RK4 integration for N=1 ---
giving the values of u1 for each time step
-
a proc to evaluate the RHS function, f1,
for specified values of t,u1.
(In this 'logistic' equation case,
there is no dependence of f1 on t --- only on u1 ---
and the constants r and k.)
The latter proc ('deriv', say) is called several times by
the former proc ('rk4', say), for each time step.
METHOD of PLOTTING
THE POPULATION CURVE
on the TK CANVAS :
After a solution, we have the solution function
u1 for a sequence of equally-spaced time values.
We use time, t, as the horizontal axis of the plot.
The time goes from zero to the end-time, tmax, specified
by the user.
As the numerical integration proceeds, we keep track
of the maximum value, umax, reached by u1 over the integration
time period.
The solution curve is plotted in a rectangular area:
A margin is to be supplied around this rectangular area,
and two axes are drawn --- a horizontal time-axis
and a vertical u-axis (population).
Min and max values are to be indicated on the ends of the 2 axes.
Intermediate tic-marks and tic-labels may also be supplied.
It would be nice for the GUI to provide 2 buttons by which
the user can specify 2 colors for:
A 'plot' proc (with auxiliary procs) performs the plot of
the solution when the user clicks on a 'Plot' button of the GUI.
This 'plot' proc uses the 'world-coordinates' --- the
0 to tmax values and the 0 to umax values --- to draw the
plot within an area of about tmax by umax in world coordinates.
Actually, we augment this world-coordinates rectangular area
by providing a margin of about 0.1*tmax and 0.1*umax
on the left and right and on the top and bottom, respectively,
of the plot area.
A proc is provided which maps the plot area limits in
world coordinates --- say
UpperLeftCorner: ( -0.1*tmax , 1.1*umax )
LowerRightCorner: ( +1.1*tmax , -0.1*umax )
to the corners of the plot area in pixel coordinates:
UpperLeftCorner: (0,0)
LowerRightCorner: (ImageWidthPx , ImageHeightPx)
We may allow the user to determine the ImageWidthPx and ImageHeightPx
values (in pixels) by letting the user resize the window, which
will cause the Tk 'canvas' widget to resize --- and we will query
the current canvas size to get ImageWidthPx and ImageHeightPx.
Hence we avoid having to use widgets on the GUI by which the user
can specify the size of the plot area.
The 'plot' proc uses 2 procs --- Xwc2px and Ywc2px ---
to convert the world coordinates of each point --- such as
the end-points of the axes and the end-points of line-segments
connecting successive plot points --- to pixel coordinates.
The pixel-coordinates are used in 'create line' and
'create text' commands to draw the plot on the canvas.
THE GUI LAYOUT :
Based on the notes above, the Tk GUI should allow the user to specify
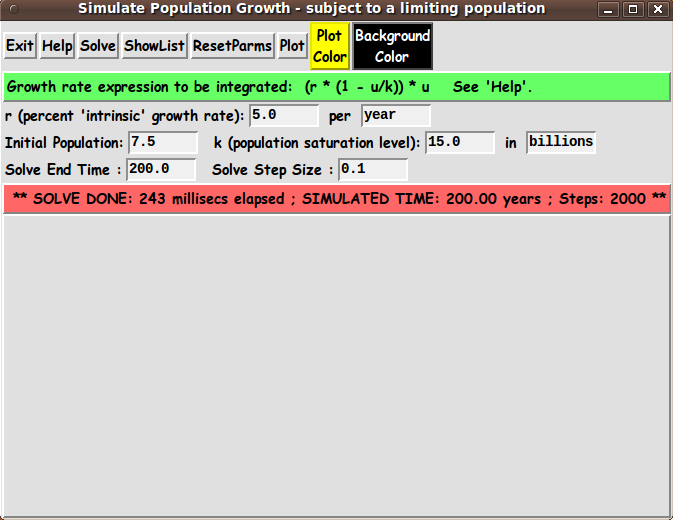
There is to be a 'Solve' button to perform a solution
when the user is ready to use these parameters.
A 'ShowList' button can be used to show the list of
solution values --- t(i), u1(t(i)) ---
in a popup window.
There are also to be 2 buttons by which to call up an
RGB-color-selector GUI by which to specify the 2 colors
for the animation drawing on the canvas.
In addition, on the GUI, there is to be a 'Plot'
button to generate the population plot.
One way the user can specify all these parameters is indicated by
the following 'sketch' of a layout for the GUI.
In the following sketch of the GUI:
|