FE 'tkGooie' Utilities'PHYSICStools' group
1D Collision of
|
FE 'tkGooie' interface to simulate 2 colliding masses A larger, hi-res image is below. |
FE Home Page >
FE Downloads Page >
FE 'tkGooies' Description Page >
FE 'tkGooies' 'PHYSICStools' Page >
This
'tkAnimateCollisionOfTwoRigidMasses_1D'
tkGooie Page
|
INTRODUCTION to Tcl-Tk script For at least 5 years now (about 2011 to 2016), I have had it on my Tk-scripts-to-do list to implement Tcl-Tk GUI scripts that perform numerical-integration of the ODE's (ordinary differential equations) that describe some dynamic physics configurations of classical mechanics --- as well as handling some non-physics applications. I had in mind the differential equations describing
Recently (July 2016), I finally implemented a Tk script to simulate a single oscillating pendulum. The script integrates the 'nonlinear' second-order differential equation that can simulate the motion of a wide-swinging pendulum --- that is, there is no need to restrict the situation to small angular oscillations of the pendulum. That Tk GUI script allowed for animating a representation of a pendulum arm-and-bob --- on a Tk 'canvas' widget. I also implemented a Tk script to simulate a bouncing rigid ball (such as a golf ball). However, there are some other types of dynamic 'problems' in physics that do not require numerical integration of differential equations --- for a solution --- and for an animation. That is, some physics 'problems' have an algebraic solution --- and that algebraic solution can be used to generate an animation of the components in the 'problem'. Examples include collision problems of masses where it is assumed that there are no frictional losses --- and where the algebraic solution can be derived based on a physical 'law' such as conservation of momentum and/or conservation of energy. One such 'problem' involves collision of 2 masses where the 2 masses separate after the collision (Wikipedia link). Another such 'problem' involves collsion of 2 masses where the 2 masses stick together after the collision (Wikipedia link). There are many animated GIF files on the internet depicting these types of collisions for one specific case of the values of the masses and the initial velocities. But I wanted to provide a 'tkGooie' by which the user can experiment with different mass values and initial velocity values. I wanted to handle the case where the two masses are moving in the same direction (one over-taking the other) --- as well as the usual cases of masses moving toward one another --- or one mass being at rest. And I wanted to provide these new 'physics tools' via a new 'PHYSICStools' drawer in the main toolchest of the FE 'tkGooies' system:
via a new 'PHYSICStools' toolchest:
This page is meant to deal with the first of these 2 collision 'problems'. The 'collide-and-stick-together' situation is handled on another page. NOTATION and EQUATIONS There are some PDF files on the internet that present (using nice notation) a nice, compact derivation of the equations for the velocities resulting from a so-called 'elastic' collision of 2 masses, for given pre-collision velocities. But links like these can 'go dead' over time. Since you can do a lot of web searching and not find a satisfactory presentation, below is a presentation that may save you some time. The following notation is typically used in many physics documents:
The GUI for this 'problem' should allow the user to specify m1, m2, u1, u2. Then the Tk GUI script should compute the algebraic expressions for v1 and v2. See the expressions below. The velocities u1, u2, v1, v2 can be used to animate the motions of the two masses, before and after the collision. We assume a 'conservative system'. By that we mean that the motion and collision of the 2 masses are modeled under the following assumptions.
The following 2 equations give the values of v1 and v2. |
v1 = ((m1 - m2)*u1 + (2*m2*u2)) / (m1 + m2)
v2 = ((m2 - m1)*u2 + (2*m1*u1)) / (m1 + m2)
|
These 2 equations can be derived from the 2 equations for conservation of momentum and conservation of energy: |
m1*u1 + m2*u2 = m1*v1 + m2*v2
m1*u1^2 + m2*u2^2 = m1*v1^2 + m2*v2^2
|
by using a little algebraic manipulation and the fact that a^2 - b^2 = (a + b) * (a - b) SOME DIFFERENT NOTATION: The above symbolism for the velocities can be confusing. It helps to remember that the subscripts 1 and 2 are indicative of masses 1 and 2. So the u1 and v1 velocities are for mass1 and the u2 and v2 velocities are for mass2. To make this a little clearer (during the discussions below), we can use V1 to denote velocities of mass1 and V2 to denote velocities of mass2. Then we will use
where tb denotes times BEFORE the impact and ta denotes times AFTER the impact. In other words,
u_ is an abbreviation for V_b and
v_ is an abbreviation for V_a where the underscore represents 1 or 2 (the masses). In other words, we are using 1,2,a,b with m,V rather than 1,2,u,v with m. (Not really better, perhaps.) The equations above for the 'after-velocities' become |
V1a = ((m1 - m2)*V1b + (2*m2*V2b)) / (m1 + m2)
V2a = ((m2 - m1)*V2b + (2*m1*V1b)) / (m1 + m2)
|
Some derivations use this type of notation but use 'i' in place of 'b' and 'f' in place of 'a' --- where 'i' represents 'initial' and 'f' represents 'final'. MY GOALS FOR THE GUI: The GUI should allow the user to enter various values for
In addition, the GUI should allow the user to specify the width of the image area in pixels, say ImgWidthPx. (This allows for precise control of the image size.) The GUI should provide 2 buttons by which the user can specify 2 colors for:
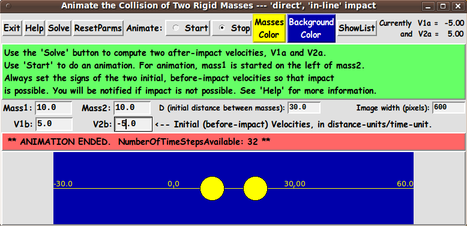
When the mass and velocity parameters are ready, the GUI is to provide a 'Solve' button by which the user can trigger the calculation of the after-impact velocities, V1a and V2a. After V1a and V2a are calculated and the user has readied the D parameter, the image width (in pixels), and the 2 colors, the user can click on a 'Start' radiobutton to start the animation. The user can click on a 'Stop' radiobutton to stop the animation, if it is still going. The GUI is to include a 'Help' button by which the user can get information on how the GUI can be used. And the GUI can include a 'ResetParms' button --- by which the user can reset the values of m1, m2, V1b, V2b, and D to their initially-displayed values. --- To evaluate any further requirements that we may need for the GUI, it is helpful to know some of the details of the method of implementing the animation Some details follow. SOME DETAILS OF THE ANIMATION PROCESS : The details of doing the drawing of the animation get rather complicated because the user can specify positive or negative velocities. If the 'before' velocities are both positive or both negative, it may take a long time for the impact to occur --- or impact may not be possible. The animation logic needs to check for the latter situation. To model the before-impact and after-impact movement within the image area, the time and place of the impact need to be computed. Then limits, Xmin and Xmax, in 'world-coordinates' need to be computed so that the animation can be drawn in such a way that the before-impact and after-impact motion can be drawn within the specified image width. The limits, Xmin and Xmax, in world-coordinates need to be mapped to the left and right pixel-coordinates, 0 and ImgWidthPx. This will allow the before-impact, impact, and after-impact motion of the 2 masses to proceed within the image area. A time-step size, h, may be automatically computed for the user in order that the animation proceeds smoothly. The initial distance, D, between the 2 masses may need to be adjusted to avoid an animation that proceeds too slowly. In addition, we use the value of the 2 masses, m1 and m2, to determine the radii of the 2 circles that are drawn to indicate the magnitude of the 2 masses. The way that these 2 radii are determined, in world-coordinates, can be rather involved. See the comments in the 'animate' proc for details on the various aspects of implementing the animation. THE GUI LAYOUT : From the discussion above, we see that the Tk GUI should allow the user to specify m1, m2, V1b, V2b from which V1a and V2a can be calculated. There is to be a 'Solve' button --- to calculate V1a and V2a. --- For the animation, some other parameters may be required. For example: The GUI can let the user specify the width of the image area in pixels, say ImgWidthPx. The GUI can provide 2 buttons by which the user can specify 2 colors. And the GUI may allow the user to specify D ---- an initial distance between m1 and m2. Then, on the GUI, there can be 'Start' and 'Stop' radiobuttons to start and stop an animation run. The time-step and speed of animation: This script may use the velocities --- V1b,V2b,V1a,V2a ---- to calculate a time-step, 'h', that gives smooth animation. (Thus we avoid the need to supply a widget on the GUI for time-step.) The time-step, 'h', may be used to control the real-time speed of the animation. To allow the user to speed-up or slow-down the animation, there could be a Tk widget ('entry' or 'scale') by which to specify a wait-time (in millisecs) between computing and displaying the new positions of the 2 circles. This would be an alternative to using a wait-time value calculated from the user-selected time-step, h. For now, we may simply calculate the animation wait-time based on the time-step, h. We may also accumulate the animation data --- t(i), x1(t(i)), and x2(t(i)) --- the location of the two masses during the animation --- in array variables. A 'ShowList' button may be used to show a table of these values. This data could conceivably be used in other applications --- such as an 'xy' plot utility. 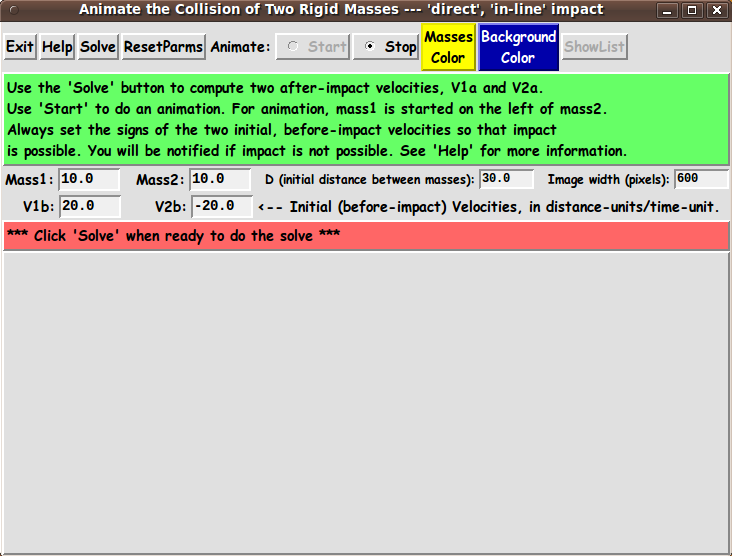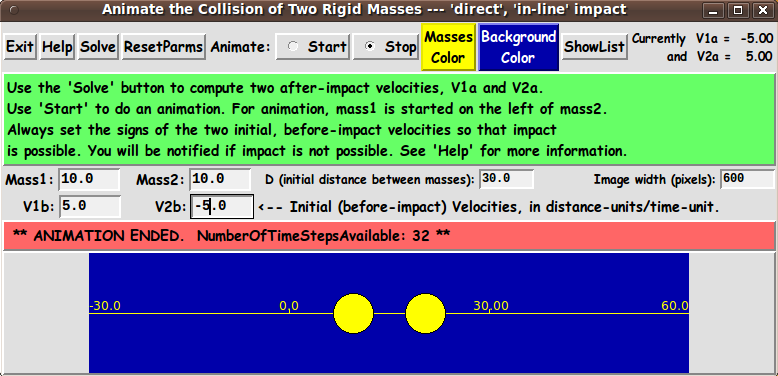--- One way the user can specify all these parameters is indicated by the following 'sketch' of a layout for the GUI. In the following sketch of the GUI: |
SQUARE BRACKETS indicate a comment (not to be placed on the GUI).
BRACES indicate a Tk 'button' widget.
UNDERSCORES indicate a Tk 'entry' widget.
A COLON indicates that the text before the colon is on a 'label' widget.
CAPITAL-O indicates a Tk 'radiobutton' widget.
CAPITAL-X indicates a Tk 'checkbutton' widget (if any).
Vertical bars (and horizontal hyphens) outline a 'canvas' widget.
If there are scrollbars:
Less-than and greater-than signs indicate the left and
right ends of a horizontal 'scrollbar'.
Capital-V and Capital-A letters indicate the bottom and
top ends of a vertical 'scrollbar'.
Here is the sketch:
FRAMEnames
VVVVVVVVVV
------------------------------------------------------------------------------------------
Animate the Collision of Two Rigid Masses --- 'direct', 'in-line' impact
[window title]
------------------------------------------------------------------------------------------
.fRbuttons {Exit} {Help} {Solve} {Reset Animate: O Start O Stop {Masses {Background {Show [a label here
Parms} Color} Color} List} for V1a,V2a]
.fRguide [ ... A description of the equation(s) or solution technique goes here, in a label widget. ... ]
.fRmasses Mass1: 10.0___ Mass2: 1.0__ D (initial distance between masses): 10___ Image square (pixels): 300__
.fRinit V1b: 2.0__ V2b: 0.0__ <-- Initial (before-impact) Velocities, in distance-units/time-unit
.fRmsg [ .......... Messages go here, in a label widget .......................... ]
.fRcanvas |-----------------------------------------------------------------------------|
| |
| [This area is to contain a non-scrollable canvas widget in which |
| the animation is to be drawn. |
| |
| The canvas widget is centered at the top of this area.] |
| |
| |
| |
| |
|-----------------------------------------------------------------------------|
|
GUI components: From the GUI 'sketch' above, it is seen that this GUI layout consists of about
The GUI (a screenshot) To implement this Tk GUI script, I fetched the
'tkSimulateBouncingBall' script that had most of these GUI elements and converted it to this 'tkAnimateCollisionOfTwoRigidMasses_1D' script. I ended up with the GUI seen in the following image. |
|
This is the GUI as it first appears. As the message in the middle of the GUI indicates, the user can take the defaults for all the parameters and simply click on the 'Solve' button to calculate the two 'after-velocities'. Then the user can click on the 'Start' radiobutton to start an animation based on the mass values, velocity values, and D. When I clicked on the 'ShowList' button, a list of computed results from an animation --- time, x1, x2 --- appeared for hundreds of time steps and corresponded to the default initial conditions. --- Note that you can use the 'ShowList' button to generate columns of decimal numbers that can be copied-and-pasted into a text-editor window. The editor can be used to save the data to a text file. Then that text file can be edited (to remove or comment out the header and trailer text) and fed into the plot utility at
tkGnuplotXY_2or3colsFromFile to get a plot of the height and/or velocity functions versus time. --- To give you an idea of what the animation image area looks like, here is a 'screenshot'. |
|
Before clicking the 'Start' button for this animation, I could have used the 2 color buttons to call up a color selector GUI to set color of the masses to white and the background color to black, for example. --- HELP TEXT The 'Help' button on the GUI shows extensive text describing this utility, in a popup window with scrollbars for the text area. DESCRIPTION OF THE CODE Below I provide a link to the Tk script code for this 'tkAnimateCollisionOfTwoRigidMasses_1D' utility. For this Tk script, I follow my usual 'canonical' structure for Tk code: |
0) Set general window & widget parms (win-name, win-position,
win-color-scheme, fonts, widget-geometry-parms, win-size-control,
text-array-for-labels-etc).
1a) Define ALL frames (and sub-frames, if any).
1b) Pack ALL frames and sub-frames.
2) Define & pack all widgets in the frames, frame by frame.
Within each frame, define ALL the widgets. Then pack the widgets.
3) Define keyboard and mouse/touchpad/touch-sensitive-screen action
BINDINGS, if needed.
4) Define PROCS, if needed.
5) Additional GUI initialization (typically with one or more of
the procs), if needed.
|
This Tk coding structure is discussed in more detail on the page A Canonical Structure for Tk Code --- and variations. This structure makes it easy for me to find code sections --- while generating and testing a Tk script --- and when looking for code snippets to include in other scripts (code re-use). I call your attention to step-zero. One thing that I started doing in 2013 is using a text-array variable --- named 'aRtext' --- for text in labels, buttons, and other widgets in the GUI. This can make it easier for people to internationalize my scripts. I will be using a text-array like this in most of my scripts in the future. Experimenting with the GUI As in all my scripts that use the 'pack' geometry manager (which is all of my 100-plus scripts, so far), I provide the four main 'pack' parameters
on all of the 'pack' commands for the frames and widgets. That helps me when I am initially testing the behavior of a GUI (the various widgets within it) as I resize the main window. I think that I have used a nice choice of the 'pack' parameters. In particular ... The labels and buttons and entry widgets stay fixed in size and relative-location as the window is re-sized --- while the area containing the 'canvas' expands/contracts as the window is re-sized. You can experiment with the '-side', '-anchor', '-fill', and '-expand' parameters on the 'pack' commands for the various frames and widgets --- to get the widget behavior that you want. --- Additional experimentation with the GUI: You might want to change the fonts used for the various GUI widgets. For example, you could change '-weight' from 'bold' to 'normal' --- or '-slant' from 'roman' to 'italic'. Or change font families. In fact, you may NEED to change the font families, because the families I used may not be available on your computer --- and the default font that the 'wish' interpreter chooses may not be very pleasing. I use variables to set geometry parameters of widgets --- parameters such as border-widths and padding. And I have included the '-relief' parameter on the definitions of frames and widgets. Feel free to experiment with those 'appearance' parameters as well. --- Note that the color buttons call on a color-selector-GUI script to set the colors. You can make that color-selector script by copying-and-pasting the code from the page offering 'a non-obfuscated color selector GUI', on this site. Some comments and code at the bottom of this 'collision animation' Tk script explain how you can implement the RGBcolor selector. Some features in the code There are plenty of comments in the code, to describe what most of the code-sections are doing. You can look at the top of the PROCS section of the code to see a list of the procs used in this script, along with brief descriptions of how they are called and what they do. --- Here is a brief overview of the procs of the script. |
- 'solve' - called by the 'Solve' button.
- 'animate' - called by a click on the 'Start' animation radiobutton.
- 'show_list' - called by the 'ShowList' button
- 'setMappingVars_for_px2wc' - called by proc 'animate'.
- 'Xwc2px' - called by proc 'animate'.
- 'Ywc2px' - called by proc 'animate'.
- 'set_mass_color1' - called by the 'MassesColor' button.
- 'set_background_color2' - called by the 'BackgroundColor' button.
- 'update_color_button' - sets background & foreground color of
either of the 2 color buttons ---
called by the 2 'set_*_color*' procs and in the
'Additional GUI Initialization' section,
to initialize colors on the 2 color buttons.
- 'advise_user' - called by the 'solver' and 'animate' procs.
- 'reset_parms' - called by the 'ResetParms' button and in the
'Additional GUI Initialization' section,
to initialize the parms.
- 'edit_inputs' - called by 'solve' and 'animate' procs
- 'decimal_check' - called by 'edit_inputs' proc
- 'popup_msgVarWithScroll' - called by the 'Help' button.
|
The most complicated code is in the 'animate' proc. See the comments in these procs for details on their implementation. A fervent hope It is my hope that the copious comments in the code will help Tcl-Tk coding 'newbies' get started in making GUI's like this. Without the comments, potential young Tcler's might be tempted to return to their iPhones and iPads and iPods --- to find 'animated GIFs' of an image of Donald Trump morphing back and forth between a look-alike image of Mussolini or Hitler --- a 'Trumpolini' or 'Trumpler' animation. Or, potential Tcler's may spend time trying to find animated-GIF's of an image of Hillary Clinton morphing back and forth between a look-alike image ... like what? ... a squawking parrot? If you cannot find such an animated-GIFs, then you can create one using the 'wheeeMorph' utility of the FE 'tkGooies' system. But, before doing that, try the following code. The Tcl-Tk CODE : Here is a link to CODE for the script 'tkAnimateCollisionOfTwoRigidMasses_ 1D.tk' With your web browser, you can 'right-click' on this link --- and in the menu that pops up, select an item like 'Save Link Target As ...' --- to save this file to your local computer. Then you can rename the file to remove the '.txt' suffix. Make sure that you have execute permission set on the file --- in order to execute the script. SOME POTENTIAL ENHANCEMENTS: Some features that I may add to this Tk script --- or implement in a separate Tk script:
--- There will probably be more enhancements that I may think of in the future, although some enhancements might be more suitable for putting in a separate Tk script --- perhaps using somewhat different methods or a different GUI design than were used in this script. --- For those who might want to go ahead and add enhancements: To help out in making scripts like this, here is a page that provides sources of Tcl-Tk code snippets by providing links to various 'tkGooies' scripts (and wiki.tcl.tk scripts) that can make it relatively quick work to compose
And when you get to the testing-and-debugging phase in development of a script, here is a page that describes the wonderfulness of the 'wish' 'stack trace' facility which can make the testing-and-debugging go relatively quickly and painlessly. IN CONCLUSION There's a lot to like about a utility that is 'free freedom' --- that is, no-cost and open-source so that you can modify/enhance/fix it without having to wait for someone else to do it for you (which may be never). I hope to provide more free scripts that can be used to demonstrate physics principles (and Tk coding techniques) --- scripts that could be used in a classroom or self-teaching setting. As I have said on other 'tkGooie' pages of this FE web site ... A BIG THANK YOU to Ousterhout for starting Tcl-Tk, and a BIG THANK YOU to the Tcl-Tk developers and maintainers who have kept the simply MAH-velous 'wish' interpreter going. |
|
Bottom of this page for
To return to a previously visited web page location, click on the
Back button of your web browser a sufficient number of times.
OR, use the History-list option of your web browser.
< Go to Top of Page, above. >Page history:
This FE web page was created 2016 Jul 23.
NOTE: |